Vielen Dank für die bisherigen Hinweise. Die Lösung ist mir aber leider immer noch rätselhaft, daher habe ich unten bei "Ergänzung" die verbleibende Problematik noch einmal in Kürze beschrieben
(Achtung: Lang - Es ist auch ok, gleich zur Hauptfrage unten zu gehen)
Hallo,
mein Bruder macht ein Ingenieurs-Studium, allerdings fällt ihm Mathe für Ingenieure schwer.
Ich selbst habe Interesse und Spaß an Mathe und unterstütze meinen Bruder beim Lernen. Da ich aber BWL (also kein Ingenieurs-Fach) studiert habe, muss ich mir die Inhalte selbst erarbeiten. An vielen Stellen gelingt mir dies, am manchen Stellen, so wie hier, komme ich/kommen wir aber nicht weiter und ich hoffe, dass uns jemand helfen kann.
Problem: Wir haben eine Aufgabe und Lösungen dazu, können aber nur die ersten beiden Teile lösen. Beim dritten Teil der Aufgabe ( c. ) können wir uns den Lösungsweg nicht erklären.
Aufgabenstellung:
Quelle: Aufgabensammlung - Mathematik I
(MA1-Aufgabensammlung, Stand: November 2014
Department Fahrzeugtechnik und Flugzeugbau, HAW-Hamburg)
Gegeben ist das folgende Polynom 3. Grades:
 Die Funktion f(x) besitzt an der Stelle x=5 eine Nullstelle.
Die Funktion f(x) besitzt an der Stelle x=5 eine Nullstelle.
Die folgenden Unterpunkte sind zu lösen:
a. Berechnen Sie alle Nullstellen des Polynoms f(x). - Dies konnten wir lösen.
Lösung: x1 = 5; x2 = 1,5; x3= -0,75
b. Formulieren Sie das Polynom f(x) so um, dass es an der Stelle x=4 entwickelt vorliegt. - Dies konnten wir schließlich auch lösen.
Lösung: 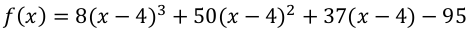
c. Geben Sie die Parabel an, die sich an das Polynom f(x) im Punkt x=4 anschmiegt und
berechnen Sie den Scheitelpunkt dieser Parabel.
Hinweis: Sie können zur Lösung Aufgabenteil b von zuvor nutzen.
Lösung: 
Hauptfrage: Wie kommt man auf den Lösungsansatz bei Teil c. und schließlich auf die Lösung?
Zusatzkommentare:
- Wir haben Videos von Daniel Jung zur Taylor-Approximation angesehen, finden darin aber keinen Lösungsansatz.
- Im Lehrbuch (Lothar Papula; Mathematik für Ingenieure und Naturwissenschaftler; Band 1) wird der Gaußsche Algorithmus kurz angesprochen und dargestellt. Mit dem Hinweis auf hohen Rechenaufwand wird der Algorithmus als "für die Praxis wenig geeignet" nicht weiter mit Beispielen dargestellt. Stattdessen wird das Interpolationspolynom von Newton erläutert und die Berechnung der Koeffizienten nach dem Steigungs- oder Differenzschema erläutert. Leider finden wir auch hierin keinen Ansatzpunkt. Auch hiermit konnten wir die Lösung nicht finden.
Nebenfragen:
- Warum wird extra darauf hingewiesen, dass man zur Lösung Aufgabenteil b. benutzen kann (soll?)
- Könnte man die Lösung nicht auch aus der Gleichung zu a. ableiten?
- Bei einer Approximation durch eine Parabel (Polynom 2. Grades) werden 3 Stützstellen benötigt. Ich hatte z.B. versucht, mit der bekannten und den zwei in a. berechneten Nullstellen das Interpolationspolynom von Newton aufzustellen, habe aber ganz andere Ergebnisse erhalten als in der Lösung zu c.
- Wie wähle ich diese Stützstellen für diese Aufgabe aus und warum genau diese?
- Würde es sinvoll sein, die Gleichung aus Teil b. zu nehmen und dann die Punkte (4; -95) sowie die zwei umliegenden(bekannten) Nullstellen zu verwenden?
- Wenn ich die Funktionsplots zu allen Gleichungen miteinander vergleiche, vermute ich, dass zur Lösung der Punkt (4; -95) und die Steigung an dieser Stelle herangezogen werden, um daraus eine Parabel zu ermitteln, die ebenfalls durch diesen Punkt geht und dort die gleiche Steigung aufweist. - ABER: Es gibt hier nicht nur eine Parabel, die diese beiden Eigenschaften aufweist, sondern unendlich viele. Man könnte selbst eine Normalparabel so verschieben, dass sie sich im Punkt (4;-95) "anschmiegt", aber diese Lösung ist offenbar nicht gesucht.
Ich hoffe, es kann uns jemand bei unseren Fragen helfen. - Der wichtigtste Punkt ist der Lösungsansatz und der Weg dahin. Die übrigen Kommentare und Fragen sollten beim Verständnis unterstützen, sind aber nicht so wichtig, wie die Hauptfrage.
Jetzt schon einmal vielen Dank fürs Lesen und für Eure Unterstützung.
Ergänzung:
Danke für den Vorschlag mit den Funktionsplots. Das hatte ich mit Funktion und vorgegebener Lösungs-Approximationsfunktion auch gemacht. Das veranschaulicht das Thema, hat aber leider bei der Lösung auf dem Rechenwege noch nicht weitergeholfen.
a) Die folgende Funktion

ergibt an der Stelle X=4 entwickelt folgende Funktion:
b)
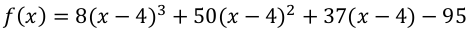 (Den Lösungsweg bis hierhin konnte ich nachvollziehen.)
(Den Lösungsweg bis hierhin konnte ich nachvollziehen.)
Mit Hilfe "der Ergebnisse aus b) " soll die Parabel berechnet werden, die sich an der Stelle x=4 am besten anschmiegt.
Für die Methode der Taylor-Approximation habe ich die erste und zweite Ableitung gebildet und zwar von der Funktion, die ich als Ergebnis aus Aufgabenteil b) erhalten hab.
Erste Ableitung von b) :
f'(x)= 4(x−4)2−+100(x-4)+37 bzw. f'(x)=24x2−92x+21
Zweite Ableitung von b) :
f''(x) = 48x-92
Für die Aufstellung der Taylor-Reihe habe ich folgendes gemacht: Ich habe die Werte der Funktion bzw. ihrer Ableitungen an der Stelle x=4 berechnet und diese Werte in die Formel für die Taylor-Reihe eingesetzt. Dieses habe unter Verwendung der Ableitungen der Funktion bis zur zweiten Ableitung vorgenommen, um ein Approximationspolynom zweiten Grades zu erhalten.
Bei der Funktion und ihrer Ableitungen an der Stelle x=4 blieb als Wert immer nur noch das jeweilige Absolutglied übrig (-95 / 37 / 100) so dass das mit der Taylor-Reihe erstellte Approximationspolynom sich wie folgt darstellte:.
fT(x) = -95 +(37/1)(x-4) +(100/2)(x-4)2
2
Es erscheint mir schon seltsam, dass das Näherungspolynom nur aus den Gliedern der Ursprungsgleichung der zweiten und ersten Potenz und dem Absolutglied besteht und ausserdem von der vorgegebenen Lösung

abweicht.
Wer kann mir dabei helfen, den/die Fehler zu finden?
Herzlichen Dank an alle!

 Die Funktion f(x) besitzt an der Stelle x=5 eine Nullstelle.
Die Funktion f(x) besitzt an der Stelle x=5 eine Nullstelle.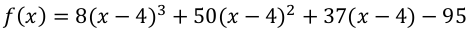

Die Ursprungsfunktion f(x) = 8*x^3 - 46*x^2 + 21*x + 45.
Die an der Stelle x=4 entwickelte Funktion ist f1(x)=8*(x-4)^3+50*(x-4)^2+37*(x-4)-95
Für die in der Aufgabenstellung vorgegebene Taylor-Approximation (s. oben im Ursprungs-Beitrag - Teil c. unter Verwendung des Ergebnisses von b. d.h. unter Verwendung der an der Stelle x=4 entwickelten Funktion) berechne ich die Werte der Funktion entwickelten Funktion f1(x) und ihrer Ableitungen an der Stelle x=4 und erhalte:
f1(4) = 8*(4-4)^3 + 50*(4-4)^2 + 37*(4-4) - 95 = 0 + 0 + 0 -95 = -95
f1'(x) = 24*(x-4)^2 + 100*(x-4) + 37
f1'(4) = 24*(4-4)^2 + 100*(4-4) + 37 = 0 + 0 + 37 = 37
f1''(x) = 48*(x-4) + 100 oder nach Vereinfachung f1''(x) = 48*x - 92
f1''(4) = 0+100 = 100 bzw. f1''(4) = 48 * 4 -92 = 100
Die Taylor-Reihe bis zur zweiten Potenz ergibt dann nach meiner Rechnung:
f[2](x) = -95 + (37/1)*(x-4) - (100/2) (x-4)^2 --> f[2](x) ist gemeint als Polynom zur Funktion vom Grade "2"
Umgestellt und vereinfacht erhalte ich daraus:
f[2](x) = 50(x-4)^2 + 37*(x-4) - 95 also einfach nur das zweite, dritte und vierte Glied des Ursprungspolynoms.
Herauskommen sollte aber f(2](x) = 50+(x-3,63)^2 - 101,845.
Was habe ich falsch gemacht bzw. wie mache ich es richtig?
Schon jetzt wieder herzlichen Dank für eine Antwort.
─ striving_mind 12.01.2020 um 18:18