Stimmt NO 6 Teil B

Aufrufe: 681     Aktiv: 27.01.2020 um 09:17
2

 

 

 

ich zeige kalrer was ich meine

ic habe das Dreick rot, an die Punkt gespiel und kam das Bild A' B' C' raus

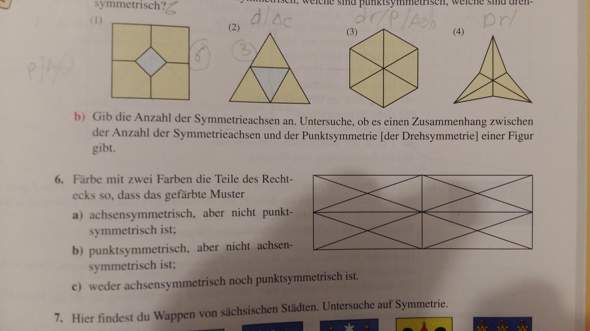
Teil a dasist beides 

 

hier wird jedes kleines Dreick Punktsymmetrisch gemacht. also 4 punktsymmetrische dreicke.

 

Diese Frage melden
gefragt

Schüler, Punkte: -155

Leider scheint diese Frage Unstimmigkeiten zu enthalten und muss korrigiert werden. City1 wurde bereits informiert.