Question

Mehrfachintegration, Gaußscher Integralsatz, Rotationsparaboloid, Volumenintegral

Aufrufe: 846 Aktiv: 17.02.2020 um 17:25

0

Aufgabenstellung:

Gegeben ist ein Rotationsparaboloid \(\mathcal{P}:=\{(x,y,z)\in \mathbb{R}^3: x^2+y^2=z,0 \le z \le 1\}\). Das stetig differenzierbare Vektorfeld \(f: \mathbb{R}^3 \rightarrow \mathbb{R}^3\) sei gegeben durch \(f(x,y,z):=(x^2-y^2z,xz^2-yz,-2xz+z^2)\). Zeigen Sie mit Hilfe des Gaußschen Integralsatzes, dass gilt \(\int_{\mathcal{P}}\langle f,N\rangle do=-\frac{2}{3} \pi \) wobei \(N\) das äußere Normalenfeld an \(\mathcal{P}\) bezeichne.

Erkenntnis:

Der Rand des Gebietes ist \(\mathcal{V}:=\{(x,y,z)\in\mathbb{R}^3:x^2+y^2=z,0<z<1\}\) und \(\mathcal{K}:=\{(x,y,z)\in\mathbb{R}^3:x^2+y^2<z,z=1\}\) und damit erhält man mit Gauß, dass \(\int_{\mathcal{P}}\langle f,N\rangle do=\int_{\mathcal{V}}div(f)dV-\int_{\mathcal{K}}\langle f,N\rangle do\). Mit \(N=(0,0,1)\) folgt \(\int_{\mathcal{K}}\langle f,N\rangle do=\pi\).

Frage:

Soweit so gut. Aber irgendwie weiß ich nicht, wie ich \(\int_{\mathcal{V}}div(f)dV = \int_{\mathcal{V}}zdV\) berechnen soll. Weder mit meiner Parametrisierung \(\gamma(r,\varphi) = (r\cos(\varphi), r\sin(\varphi), r^2), r \in (0,1), \varphi \in (0, 2\pi)\) noch mit Kugelkoordinaten komme ich auf eine vernünftige Lösung des Integrals. Habe ich etwas Grundlegendes übersehen?

Teilen Diese Frage melden

gefragt 17.02.2020 um 09:54

inaktiver Nutzer

Kommentar schreiben

1 Antwort

vt5 · Accepted Answer · 2020-02-17T16:16:05Z

Wir wählen hier Zylinderkoordinaten - oder besser gleich das Konzept der Rotationskörper (Kurzlösung siehe unten):

`"div"(f(x,y,z))=z` - wie du richtig festgestellt hast!

Für Zylinderkoordinaten brauchen wir die Funktionaldeterminate `r`, also `dV=dxdydz=r*dphidrdz`

(Siehe auch: https://de.wikipedia.org/wiki/Funktionaldeterminante)

Wodurch ist nun `r` gegeben? - nun offensichtlich haben wir mit `x^2+y^2=z` die Kreisgleichung in leicht modifizierter Form, das heißt wir identifizieren `sqrt(z)` mit dem Kreisradius (in Zylinderkoordinaten) des Rotationsparaboloids bei jeder Höhe `z`.

Wir lösen also folgendes Integral:

`int_0^1dzint_0^(sqrt(z))drint_0^(2pi)dphi"div"(f)=int_0^1dzint_0^(sqrt(z))drint_0^(2pi)dphi*z`

`=int_0^1dzint_0^(sqrt(z))dr*2pir*z=int_0^1dz[pir^2*z]_0^(sqrt(z))=int_0^zdzpi*z^2`

`=[1/3*pi*z^3]_0^1=pi/3`

Erkennen wir hingegen den Rotationskörper - dann geht es wie gesagt einfacher!

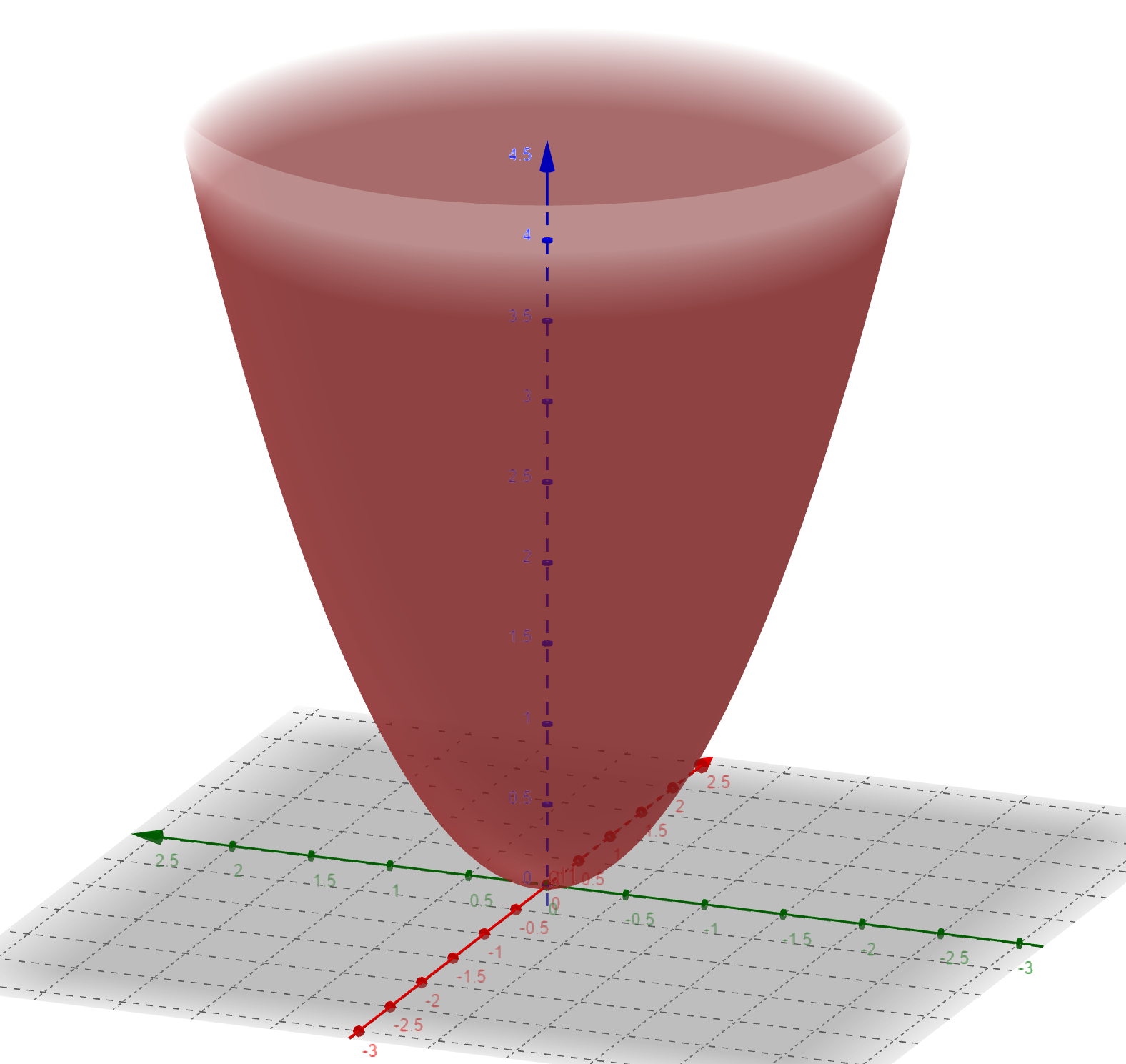
So verwenden wir die Rotationskörperformel:

`F(V)=pi*intdz*r(z)^2*g(z)` | Wobei `g(x)` eine beliebige Funktion von (ausschließlich) `z` sein kann - z.B. eine Dichte, in unserem Fall offensichtlich einfach `g(z)=z` also die Divergenz. `r(z)` gibt den Radius des Rotationskörpers in Abhängigkeit von `z` an, hier: `r(z)=sqrt(z)` - Argumentation siehe oben! `F(V)` schreibe ich, um eine volumenabhängige Funktion anzugeben.

Eingesetzt ergibt sich:

`F(V)=pi*int_0^1dz*sqrt(z)^2*z=pi*int_0^1dz*z^2=pi/3`

Berechnen wir nun `pi/3-pi=-2/3pi`, so erhalten wir das gewünschte Ergebnis.