Hallo,
die Transformation ist an und für sich nicht schwer. Die x-Koordinate wird zu r*cos(\varphi) und die y-Koordinate entsprechend zu r*sin(\varphi).
Überlege dir in welchem Bereich zum einen dein Radius laufen kann (Achtung: er muss zwischen 0 und einer positiven Zahl liegen) und zum anderen schaust du dir mal den Weg zwischen der x-Achse und der y-Achse an und überlegst dir, welcher Winkel dazwischen liegt. Den musst du dann in Verbindung mit \Pi bringen.
So erhälst du ein Doppelintegral über r und \varphi. Vergiss aber bei der Berechnung nicht die Funktionaldeterminante (die ist bei Polarkoordinaten einfach r), welche durch die Transformation immer mit berücksichtigt werden muss.
Ich hoffe, dass hilft dir erst mal...
Student, Punkte: 450
Jetzt musst du noch die x- und y-Komponenten durch deine neuen Transformation mit r und \varphi ersetzen und anschließend solltest du die entstandene Funktion integrieren können (und wieder die Funktionaldeterminante nicht vergessen!).
Du integrierst jeweils nach r und \varphi, wobei darauf zu achten, dass die Integrationsreihenfolge beachtet wird. Das soll heißen, dass zunächst das innere Integral mit den richtigen Grenzen (entweder r oder \varphi) berechnet wird und dann das äußere...
Und sorry für die späte Antwort. ─ moped_112 19.02.2020 um 23:28
Integral 0 bis pi/2 von Integral 0 bis 1 von (r*cos(p) e^((r*cos(p))^2 +(r*sin(p))^2))) * |det J(Drehmatrix| dr dp
und wenn das umformt, kommt man auf das entsprechende Integral von (r^3 cos^2(p) e^(r^2)) dr dp
Stimmt das so?
Wenn ja, habe ich es für das Beispiel verstanden.
Aber beim zweiten Beispiel nicht, denn das ist ja kein einfacher Kreis, sondern zum Einen auf der x-Achse verschoben und zum Anderen hat es die Form von einer Kardioide, also dieser Herzfunktion. ─ anonym59494 20.02.2020 um 09:56
$$ \mathrm{d}A = r \mathrm{d}r \mathrm{d}\varphi $$
und
$$ r^2 = x^2 +y^2 ,\quad x = r \cos(\varphi) $$
gilt
$$ \int_E x^2 e^{x^2+y^2} \mathrm{d}A = \int_0^{\frac {\pi}2} \int_0^1 r^3 \cos^2(\varphi) e^{r^2} \mathrm{d}r \mathrm{d}\varphi $$
Zu der 2)
Transformiere vorher schon in ein anderes Koordinatensystem, damit die Grenzen schon eine schönere Form erhalten. Nimm dafür wieder die Polarkoordinaten.
Du kannst dir merken wenn
$$ r^2 = x^2 + y^2 $$
vorkommt nutzt du fast immer Polarkoordinaten bzw in 3D Zylinderkoordinaten
wenn
$$ r^2 = x^2 + y^2 + z^2 $$
bieten sich eigentlich immer Kugelkoordinaten an (natürlich nur in 3D)
Wenn du nun die neuen Grenzen hast, kannst du eine Grenze in Abhängigkeit der anderen wählen. ─ christian_strack 20.02.2020 um 10:39
Bei der 2 würde ich sagen, dass r =3 ist, also Integral von 0 bis 3 über r.
Und da es jetzt über den gesamten Kreisbogen geht, sollte phi von 0 bis 2pi laufen oder?
Nehme ich als Funktion dann die, die in der Menge steht und ersetze hier wieder x mit rcos(phi) und y mit rsin(phi)? ─ anonym59494 20.02.2020 um 10:53

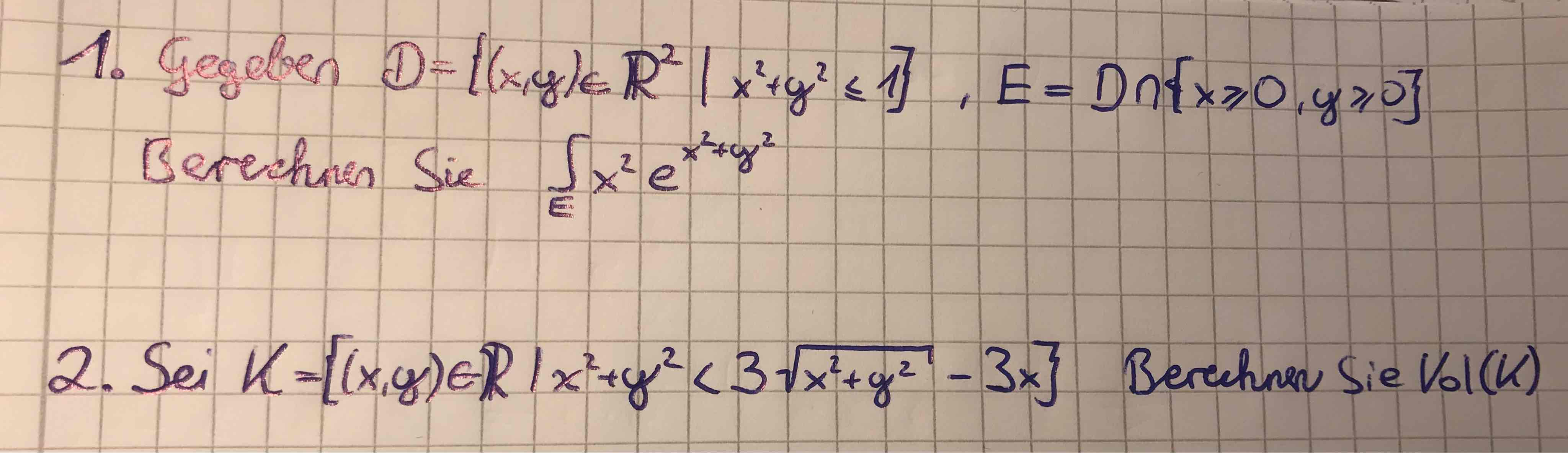
danke für deine Antwort.
Also für mich erscheint es nur sinnvoll, dass der Radius gleich 1 ist und durch die Bedingung an E sollte der Winkel gleich pi/2 sein, da es sich nur um den ersten Quadranten dreht.
Aber wie schreibt man das denn formell auf, wonach wird integriert und verändert sich die Funktion irgendwie?
Ich bin hier tatsächlich bei 0 bei dem Thema :D
─ anonym59494 19.02.2020 um 16:41