0
x wird substituiert durch x+1/2 +k
Diese Antwort melden
Link
geantwortet

scotchwhisky
Sonstiger Berufsstatus, Punkte: 12.68K
Sonstiger Berufsstatus, Punkte: 12.68K
vorher oben x=k+1 nachher x+k+1/2=k+1 ==> x=1/2
─
scotchwhisky
02.05.2021 um 12:50
Ja, aber mir ist noch nicht klar, wie ich das so umforme, dass ich für die untere Grenze eine 0 habe. Hättest du da vielleicht noch einen Hinweis?
─
user553b7a
02.05.2021 um 12:59
das war erstmal die Umformung1. Dann wird das Integral von -1/2 bis 0 ausgedrückt durch \(\int_0^{1/2}-{x \over k+1/2 -x}dx\)
─
scotchwhisky
02.05.2021 um 13:09
Woher kommt denn das negative Vorzeichen im Nenner vor dem x?
─
user553b7a
02.05.2021 um 13:45
statt x wird (-x) gesetzt, damit sich die Integralgrenzen umkehren.
─
scotchwhisky
02.05.2021 um 14:23
Okay, danke!
─
user553b7a
02.05.2021 um 15:20
wenn die Frage für dich erledigt ist, dann bitte Haken dran
─
scotchwhisky
02.05.2021 um 15:25
Doch nochmal eine kurze Frage dazu, wenn ich statt x (-x) einsetzte, dann drehen sich ja die Integralgrenzen um, aber die obere Grenze ist ja dann noch immer -1/2. Wie bekomme ich denn das negative Vorzeichen aus der Integralgrenze raus?
─
user553b7a
03.05.2021 um 14:38
Grenze -1/2 für x wird 1/2 für -x; 0 bleibt 0
─
scotchwhisky
03.05.2021 um 14:57
Aber dann steht doch im Zähler auch noch ein -x?
─
user553b7a
10.05.2021 um 09:55
dann hast du bestimmt vergessen, dass aus dx -dx wird
─
scotchwhisky
10.05.2021 um 15:32

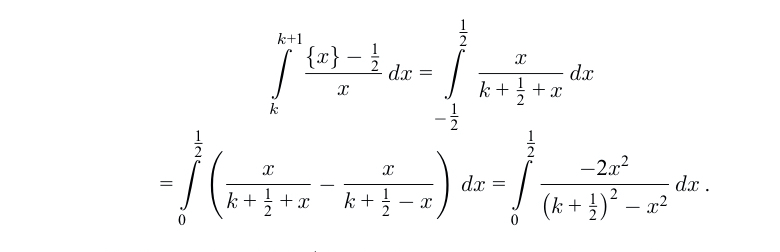
Und was passiert bei der Grenzverschiebung? ─ user553b7a 02.05.2021 um 12:29