Also:

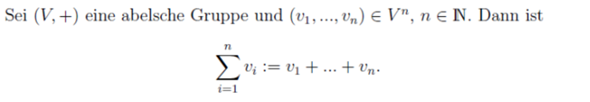
Wozu wird das erwähnt? Das sagt doch einfach aus, dass:

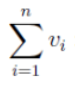
gleich der Summe aller Vektoren in einem Tupel entspricht oder? Also hier werden nicht alle Vektoren im Vektorraum aufaddiert sondern nur die, die zusammen in einem Tupel, bei V^n sind, wenn ja, warum wurde das hier erwähnt, für was?

Was ich nun nicht verstehe, für was wurde das genannt? Man hat gesagt w_j sei Element des Vektorraums V. Dann sagt man J ist eine Indexmenge, und dann wird die Summe von allen Vektoren gebildet, die in der Indexmenge J liegen, das hätte ich zumindest hiermit verstanden:

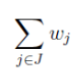
Also das man einfach sagt, man nimmt jeden Vektor, der der zur Familie mit der Indexmenge j gehört. und addiert die, wozu dann aber dieses Sigma hier:

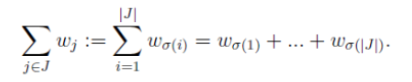
? Also warum steht da jetzt w_sigma(1) bis w_sigma(|J|)?