Um zu zeigen, dass \(x=6\) eine Nullstelle ist, reicht es, wenn du \(x=6\) einmal in die Funktion einsetzt und zeigst, dass das \(0\) ergibt. Bei dir stehen dort 3 Gleichungen, das brauchst du nicht.
Die Zeichnung ist komplett falsch, du musst dir dafür schon eine Wertetabelle oder ähnliches anlegen. Nach Gefühl lassen sich Funktionen nicht zeichnen. Außerdem muss dir Funktion bei \(x=6\) natürlich eine Nullstelle haben, das hast du ja gerade vorher gezeigt. Das ist bei dir auch nicht der Fall.
Grüße
Student, Punkte: 9.96K

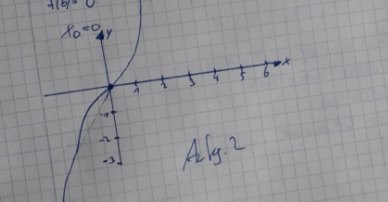
Wie mache ich da am besten die Wertetabelle? ─ usjake 22.05.2021 um 12:35