(Twitter)
1
Hallo,
leider ist Stochastik auch nicht mein Steckenpferd, deshalb bin ich mir nicht sicher ob du aus deiner gegebenen Dichtefunktion die beiden einzelnen Dichtefunktionen ableiten kann. Aber wenn wir mal davon ausgehen, dass die Dichtefunktion auch ein konstanter Wert ist
$$ f_X = c $$
und auf dem gegebenen Intervall ungleich Null sein soll, kann man die Dichtefunktionen über
$$ \int\limits_{-1}^1 c \ \mathrm{d}x = 1 $$
berechnen. Analog dann auch \( f_Y \). Was meinst du dazu?
Wenn wir dann die Dichtefunktionen haben, können wir die Verteilungsfunktionen über
$$ F_X(x) = \int\limits_{-1}^x f_X \ \mathrm{d}x $$
berechnen. Analog \( F_Y(y) \).
Grüße Christian
Diese Antwort melden
Link
geantwortet
christian_strack
Sonstiger Berufsstatus, Punkte: 29.81K
Sonstiger Berufsstatus, Punkte: 29.81K
Sieht für mich alles richtig aus. Mit meinem Ansatz wäre ich auf die selben Ergebnisse gekommen. Scheint also zu passen :)
Nun fehlt nur noch die Kovarianz. Dafür müssen die Erwartungswerte berechnet werden, denn
$$ Cov(x,y) = E(xy) - E(x)E(y) $$
Und für den Erwartungswert gilt
$$ E(u) = \int_{-\infty}^{\infty} u \cdot f_U(u) \ \mathrm{d}u $$ ─ christian_strack 20.07.2020 um 13:47
Nun fehlt nur noch die Kovarianz. Dafür müssen die Erwartungswerte berechnet werden, denn
$$ Cov(x,y) = E(xy) - E(x)E(y) $$
Und für den Erwartungswert gilt
$$ E(u) = \int_{-\infty}^{\infty} u \cdot f_U(u) \ \mathrm{d}u $$ ─ christian_strack 20.07.2020 um 13:47
das hab ich gemacht. vergessen hochzuladen. da kommt 0 raus, wenn ich es richtig gemacht haben sollte.
danke dir! ─ labis.theodoros 20.07.2020 um 20:37
danke dir! ─ labis.theodoros 20.07.2020 um 20:37
Das ist richtig :)
─
christian_strack
21.07.2020 um 09:47
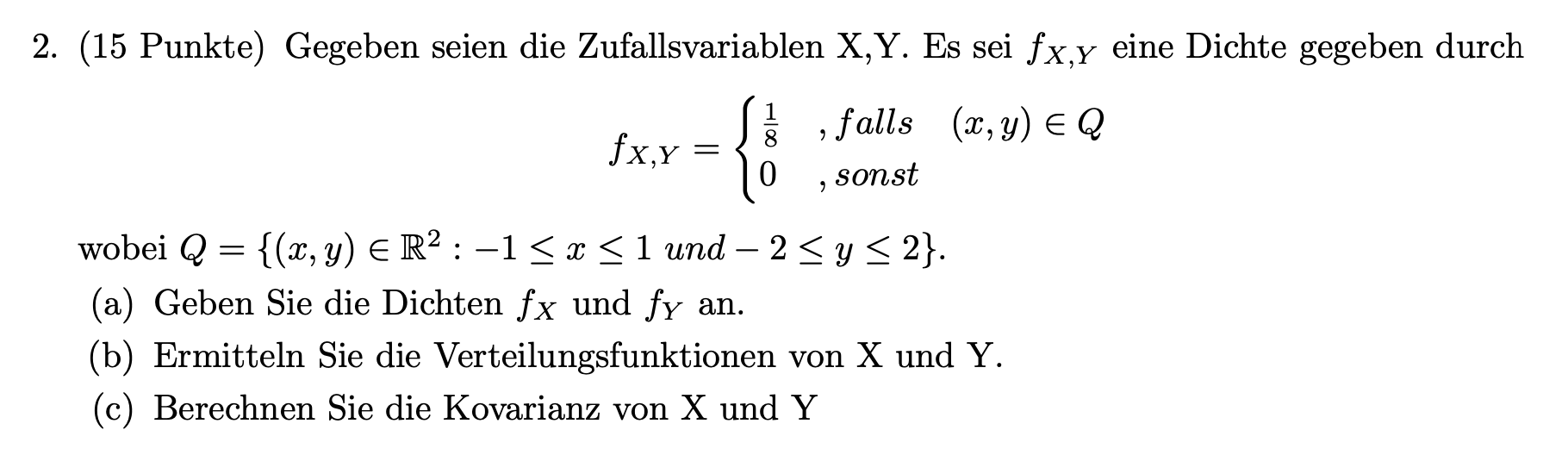
das das integral gleich 1 ist benötigt man zB um ein c zu berechnen, welcher noch zusätzlich hinzugefügt wird (aufgabe erschweren), ist aber machbar. hier sollte man in a) nur die einzelnen Dichten berechnen, hab ich geschafft. dazu kommt, dass diese Unabhängig sind und daraus ganz einfach zu erkennen ist, dass sie multipliziert wieder die gemeinsame Dichte ergeben, ─ labis.theodoros 18.07.2020 um 22:40