0
Die Formel ist doch eine gute Idee, ich hab aber 0.25 für den Flächeninhalt raus (alle Angaben ohne Gewähr). Wo Dein Fehler liegt, falls Du einen gemacht hast (und nicht ich), kann man nur sagen, wenn man Deine Rechnung kennt. Nur an der Zahl kann man ja nichts ablesen.
Wie lautet denn Deine Wendetangente und wie Deine Normale?
Wie lautet denn Deine Wendetangente und wie Deine Normale?

Diese Antwort melden
Link
geantwortet

mikn
Lehrer/Professor, Punkte: 38.93K
Lehrer/Professor, Punkte: 38.93K
Hallo ihr zwei :-) Könnte es sein, dass die Wendenormale doch nicht stimmt? Habe da: \(y=-\frac {3}{a}x+2-\frac {2}{27}a^2\)
Fläche ist bei mir 4. :-) Hoffe, ich sorge nicht für mehr Verwirrung ... ─ andima 03.02.2021 um 20:20
Fläche ist bei mir 4. :-) Hoffe, ich sorge nicht für mehr Verwirrung ... ─ andima 03.02.2021 um 20:20
@andima könntest du mir deinen Rechenweg eventuell kurz erklären? Nur damit ich nachvollziehen kann was ich falsch gemacht habe
─
anonym37b90
03.02.2021 um 22:17
Wendepunkt ( \(\frac{2}{3}a\) / \(-\frac {2}{27}a^2 \) ) Normalensteigung: \(-\frac{3}{a}\)
Einsetzen in allgemeine Geradengleichung: y=mx+b
\(-\frac {2}{27}a^2=-\frac{3}{a} \cdot \frac{2}{3}a+b\) <=> \(-\frac {2}{27}a^2=-2+b\) <=> \(b= 2-\frac {2}{27}a^2\)
\(y=-\frac {3}{a}x+2-\frac {2}{27}a^2\)
Dein Fehler liegt entweder darin, dass sich das a an einer Stelle nicht herausgekürzt hat, so dass nur die 2 übrigbleibt ... oder darin, dass du zwei Dinge zusammengerechnet hast, die man nicht zusammenrechnen darf. :-)
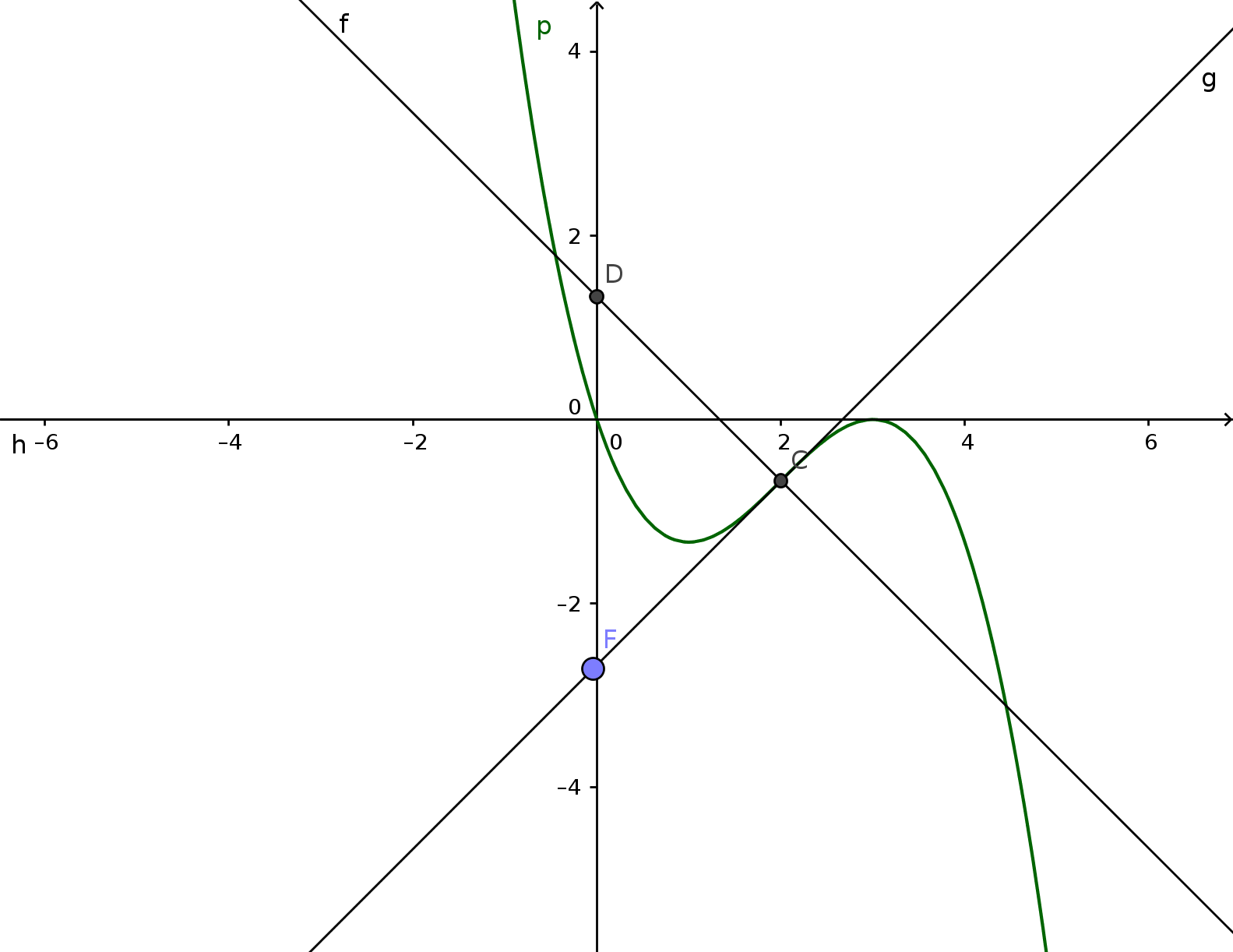
Jetzt für a natürlich 3 einsetzen. Tangente: y=x-8/3 Normale y=-x+4/3
Als Grundseite des Dreiecks wählt man den Abschnitt auf der y-Achse, dessen Länge sich durch die Differenz der y-Achsenabschnitte ergibt: 4/3-(-8/3)=4
Die Höhe des Dreiecks ergibt sich aus der Stelle des Schnittpunkts von Tangente und Normale, und das ist 2.
A=1/2*4*2=4
Nachvollziehbar?
Und jetzt muss ich ins Bett. Wünsche euch ne gute Nacht! :-)
@mikn: Gerne! War mir eine Ehre :-) ─ andima 03.02.2021 um 22:51
Einsetzen in allgemeine Geradengleichung: y=mx+b
\(-\frac {2}{27}a^2=-\frac{3}{a} \cdot \frac{2}{3}a+b\) <=> \(-\frac {2}{27}a^2=-2+b\) <=> \(b= 2-\frac {2}{27}a^2\)
\(y=-\frac {3}{a}x+2-\frac {2}{27}a^2\)
Dein Fehler liegt entweder darin, dass sich das a an einer Stelle nicht herausgekürzt hat, so dass nur die 2 übrigbleibt ... oder darin, dass du zwei Dinge zusammengerechnet hast, die man nicht zusammenrechnen darf. :-)
Jetzt für a natürlich 3 einsetzen. Tangente: y=x-8/3 Normale y=-x+4/3
Als Grundseite des Dreiecks wählt man den Abschnitt auf der y-Achse, dessen Länge sich durch die Differenz der y-Achsenabschnitte ergibt: 4/3-(-8/3)=4
Die Höhe des Dreiecks ergibt sich aus der Stelle des Schnittpunkts von Tangente und Normale, und das ist 2.
A=1/2*4*2=4
Nachvollziehbar?
Und jetzt muss ich ins Bett. Wünsche euch ne gute Nacht! :-)
@mikn: Gerne! War mir eine Ehre :-) ─ andima 03.02.2021 um 22:51
Oh ... da hab ich ja viel zu lang gebraucht für meinen Kommentar :-)
─
andima
03.02.2021 um 22:52
Und der blöde Browser hat mich nicht informiert, dass es einen neuen Kommentar gab ... :-)
─
andima
03.02.2021 um 22:54
Ja ... absolut richtig. Meine Erfahrung aus der Nachhilfe ist allerdings die, dass sich Schüler mit der Tangenten- bzw. Normalenformel deutlich schwerer tun als mit der allgemeinen Geradengleichung. Allein schon vom Einsetzen, dann noch ne Klammer ... :-) Deshalb geh ich zunächst immer erst den anderen Weg ...
Anderes Thema: Bin inzwischen ein großer Fan des Horner-Schemas ... für das du ja auch gerne einstehst ... und das völlig zurecht :-) ─ andima 03.02.2021 um 23:09
Anderes Thema: Bin inzwischen ein großer Fan des Horner-Schemas ... für das du ja auch gerne einstehst ... und das völlig zurecht :-) ─ andima 03.02.2021 um 23:09
@andima ich danke dir wirklich vielmals!! Deine Hilfe hat mir total geholfen. Und @mikn deine natürlich auch! Vielen lieben Dank euch beiden :)!
─
anonym37b90
04.02.2021 um 07:54
Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden.
Mikn wurde bereits informiert.


Meine Wendenormale hat die Gleichung -3/a +52a^2/27.
(Ich bin mir allerdings bei beiden sehr unsicher.) ─ anonym37b90 03.02.2021 um 17:48