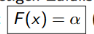Habe die Frage versucht zu formulieren, aber hat nicht ganz geklappt, bzw. ich konnte nicht ganz erklären was ich meine.
Was ich zuvor versucht habe zu erklären:
Sagen wir, wir haben den Wert 0.6, das sei das 60-Quantil.
Wenn wir nun x hätten und P(X <=x)=0.6.
Dann ist es ja im allgemeinen so, da es eine stetige Zufallsvariable ist, dass wenn ich P(X<=x) hätte berechnen wollen ich:

Diese Formel angewandt hätte.
Laut dieser Formel, müsste ich ja am Ende F(x)-F(-unendlich) rechnen.
Also Beispiel mit einer beliebigen Funktion:

z. B. will ich P(X<=3), hier würde ich bei Integral von -unendlich bis 3, am Ende also f(x) aufgeleitet zu F(x) und würde ich F(3)-F(1) berechnen.
So nun mein Problem, oben in der Folie steht:
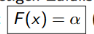
Unser alpha ist in dem Falle 0.6.
Hier sagt man, F(x)=alpha, also hier steht nicht irgendwie F(x)-F(-unendlich)=Alpha, sondern nur F(x)=Alpha, was mich hier verwirrt:
Ich weiß, dass bei diskreten Zufallsvariablen es so ist, dass ein Wert F(x) der Verteilungsfunktion F gleich der Wahrscheinlichkeit P(X<=x) entspricht, aber bei stetigen Zufallsvariablen ist es doch so, dass wenn ich die Verteilungsfunktion ableite, ich die Dichtefunktion erhalte oder?
Und da wäre es ja, logischerweise, so, dass die Dichtefunktion integriert gleich der Verteilungsfunktion ist oder?
Warum muss ich dann, wenn ich die Dichtefunktion habe und mit dieser P(X<=x) berechne, am Ende F(x_obereGrenze)-F(untereGrenze) rechnen, laut der Formel:

Da nehme ich dann ja auch nicht nur nur F(x), wie es hier steht:
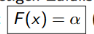
Also hier steth F(x) sei direkt alpha und alpha wird mit einem x wo gilt P(X<=x) berechnet, müsste da dann nicht stehen: F(x_obereGrenze)-F(untereGrenze)=alpha, wegen dieser <Formel:
 ?
?
(Mir ist bewusst, dass im bei diskreten Verteilungsfunktionen F(x) den WErt P(X<=x) angibt, aber hier macht das doch wenig Sinn?)