Formel umstellung

Erste Frage Aufrufe: 573     Aktiv: 28.11.2021 um 11:06
0
Hi könntet ihr mir erklären warum sich 
1.
zu
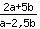
(2*a+5*b)/(1*a+-2.5*b)
kürzen lässt.

2.
zu
aber nicht.

Meine rechnung zu 1. sieht wie folgt aus ick kürze 2a²-12.5b² mit a-2,5b und komme dabei auf 2a+5b. Meine Rechnung dabei 2a²/a= 2a und -12,5b²/-2,5b= 5b also 2a+5b.

Wenn ich bei 2. allerdings nach dem selben Schmea vorgehe. Also 2a²-25b² mit a-2,5b kürze. Rechnung dann 2a²/a=2a und -25b²/-2,5b=10b also 2a+10b.
Ist das Ergebins faslch.

Stetze ich für a=4 und für b=2 ein ergibt das. 
1.
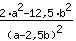
= -18

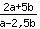
(2*a+5*b)/(1*a+-2.5*b)         = -18

2.
=-68
=-28

Woran liegt das bzw lürze ich falsch?

Die Ausgangsaufgabe bestand darin (2a-5b)^-2 * (8a²-50b²)  so weit wie einfach zu verkürzen.
Vllt könntet ihr mir ja auch einmal zeigen welche operation mit welchen rechnungenich dabei vornehmt.
Habt die Formel bis zu schluss vereinfacht bekommen. Dann versucht meine Vorgehensweise auf andere Formeln anzuwenden und bin dabei auf dieses Problem gestoßen.

Lg
Diese Frage melden
gefragt

Punkte: 10

 
Kommentar schreiben
1 Antwort
0

kürzen kann man nur Faktoren, mit Mal verbunden, nicht mit + oder -

daher muss man faktorisieren, d.h. die ausgerechnete 3.Binomische Formel im Zähler in die Klammerschreibweise zurückverwandeln. Wenn das gelingt, kann man die ganze Klammer als Faktor kürzen, wenn möglich

Diese Antwort melden
geantwortet

Punkte: 4.53K

 
schön dass du es verstanden hast, kannst das dann zukünftig auch anwenden. Sei so nett und hake die Antwort ab.   ─   honda 28.11.2021 um 11:06

Kommentar schreiben