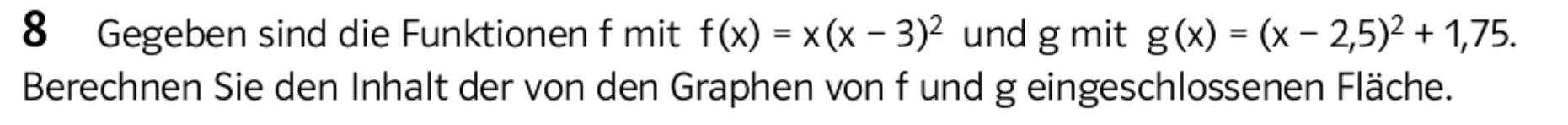Integral zwischen zwei Funktionen berechen

Erste Frage Aufrufe: 564     Aktiv: 05.12.2021 um 04:06
0

Hallo, ich bin in der 12 Klasse und übe für die nächste klausur.
Bei Aufgabe 8 komme ich nicht wirlich weiter.

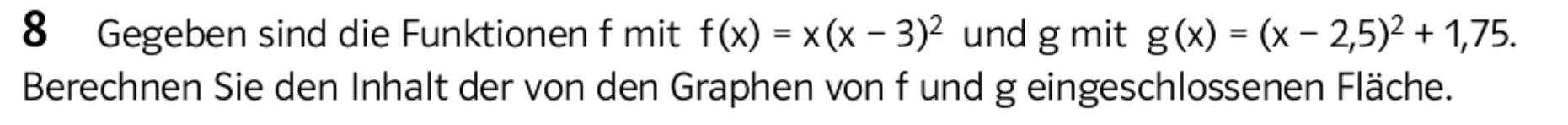
Lösung aus dem Buch

Ich habe angefangen die Schnittstellen zu berechen:
f(x)=g(x)

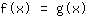
Bis dahin hab ichs verstanden. Wie man dann auf x=1,x=2 und x=4 kommt ist mir unklar. 

Ich habe dann einfach die x werte mit dem CAS Rechner ermittelt.(Würde aber gerne wissen wie man da weiter gerechnet hätte)
Nun hab ich ja meine Integral grenzen: 1 bis 4
Weiß jetzt nicht mehr wie es weiter geht.
Mit dem CAS kann ich es ,aber dort kommt auch nicht wie in der lösung 3,9 sondern 3,6 raus.
Also nochmal extra Verwirrung.
Könnte mir jemand helfen diese Aufgabe Schritt für Schritt zu lösen?
Würde mich sehr freuen und schon einaml vielen Dank.

 

Diese Frage melden
gefragt

Punkte: 10

 
Kommentar schreiben
1 Antwort
1
Du suchst ja die Nullstellen dieser Funktion. Du kannst eine Nullstelle durch Probieren finden. 1 ist sowieso ein guter Wert, den man ausprobieren kann. Dann machst du eine Polynomdivision durch $x-1$ und erhältst eine quadratische Funktion. Davon kannst du dann mit der pq-Formel (vorher normieren) die anderen beiden Lösungen berechnen. Oder du benutzt gleich die Mitternachtsformel.

Dann betrachtest du die beiden Funktion zwischen den Schnittpunkten und bestimmst, welche denn größer ist. Dementsprechend wählst du die Differenz im bestimmten Integral.

Zuletzt die Stammfunktion bestimmen und die Grenzen einsetzen.
Diese Antwort melden
geantwortet

Sonstiger Berufsstatus, Punkte: 3.96K

 
Danke für deine Antwort. Ich muss ja (wie du gesagt hast) jetzt gucken welche funktion in der grenze 1-2 und 2-4 oberhalb der anderen liegt. Um dann f(x)-g(x) oder g(x)-f(x) zu schreiben. Aber wie finde ich herraus (ohne abgebildeten graphen )welcher oberhalb liegt?   ─   usera42613 04.12.2021 um 19:43

Kommentar schreiben