0
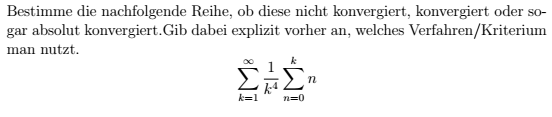
was ist mit 1/k^4?Also ist es ja schon klar, wenn k gegen unendlich geht, dann n*(n+1)/2...
─
tarsar12345
19.05.2020 um 15:14
naja dann steht da ja (1/k^4) * k*(k+1)/2 = (k+1)/(2*k^3) = k/(2*k^3) + 1/(2*k^3) = 1/(2*k^2) + 1/(2*k^3)
generell gilt: reihen deren glieder rationale funktionen sind, bei denen der grad vom nenner um mehr als 1 von dem des zählers größer ist, konvergieren ─ b_schaub 19.05.2020 um 15:18
generell gilt: reihen deren glieder rationale funktionen sind, bei denen der grad vom nenner um mehr als 1 von dem des zählers größer ist, konvergieren ─ b_schaub 19.05.2020 um 15:18
Alles klar, dann kann ich mit dem Majorantenkrit. abschaetzen um Konvergenz zu zeigen?
─
tarsar12345
19.05.2020 um 15:36
jo genau
─
b_schaub
19.05.2020 um 15:37
Vielen Dank!
─
tarsar12345
19.05.2020 um 15:43
Kannst du mir kurz erklären wie man auf die k*(k+1)/2 kommt?
─
schwierigesthema
21.05.2020 um 13:47
https://de.wikipedia.org/wiki/Gau%C3%9Fsche_Summenformel
─
b_schaub
21.05.2020 um 13:48
danke
─
schwierigesthema
21.05.2020 um 13:54