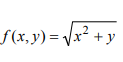0
wie hier schon super beschrieben, kannst du die Wurzel umschreiben: aus \( \sqrt{x^2+y} \) was ja eigentlich so aussieht: \( \sqrt[2]{(x^2+y)^1} \) wird \( (x^2+y)^{\frac{1}{2}} \)
nun wendest du die Kettenregel an. Einmal musst du nach x ableiten und einmal nach y.
\[ f_X (x,y) = 2x * \frac{1}{2} (x^2+y)^{\frac{1}{2}-1} = x(x^2+y)^{-0.5} = \frac{x}{\sqrt{x^2+y}} \]
\[ f_Y (x,y) = 1 * \frac{1}{2} (x^2+y)^{\frac{1}{2}-1} = \frac{1}{2}(x^2+y)^{-0.5} = \frac{1}{2\sqrt{x^2+y}} \]
achte auf die Schritte bei der Kettenregel.
nun wendest du die Kettenregel an. Einmal musst du nach x ableiten und einmal nach y.
\[ f_X (x,y) = 2x * \frac{1}{2} (x^2+y)^{\frac{1}{2}-1} = x(x^2+y)^{-0.5} = \frac{x}{\sqrt{x^2+y}} \]
\[ f_Y (x,y) = 1 * \frac{1}{2} (x^2+y)^{\frac{1}{2}-1} = \frac{1}{2}(x^2+y)^{-0.5} = \frac{1}{2\sqrt{x^2+y}} \]
achte auf die Schritte bei der Kettenregel.
Diese Antwort melden
Link
geantwortet

labis
Punkte: 113
Punkte: 113