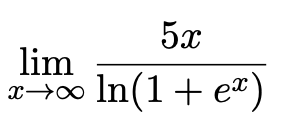Grenzwert l'Hospital - Konstante im Zähler

Aufrufe: 387     Aktiv: 29.10.2021 um 22:15
0
Der folgende Grenzwert ist mit der Regel von l'Hospital zu berechnen: 


Bekomme, nach erster Ableitung von Zähler und Nenner folgendes raus: 

(5) / (e^x / 1+e^x) 
Der Nenner geht ja immer noch gegen unendlich, sogar exponentiell. 
l'Hospital kann man auch nicht mehr anwenden, da der Zähler eine Konstante erhält. Somit müsste der Grenzwert doch 0 sein, da durch unendlich geteilt wird - aber laut Löung kommt hier die 5 raus. 
Woran liegt das? Wo ist mein Fehler?
Diese Frage melden
gefragt

Student, Punkte: 111

 
Kommentar schreiben
1 Antwort
0
Es ist $\frac{5}{\frac{\mathrm{e}^x}{1+\mathrm{e}^x}}=\frac{5(1+\mathrm{e}^x)}{\mathrm{e}^x}=\frac{5}{\mathrm{e}^x}+\frac{5\mathrm{e}^x}{\mathrm{e}^x}=\dots$

Immer erst vollständig (!) vereinfachen und dann den Grenzwert anwenden!
Diese Antwort melden
geantwortet

Selbstständig, Punkte: 30.55K

 

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Cauchy wurde bereits informiert.