1
Hier muss man die bekannten Ableitungsregeln anwenden; damit kann man sich durch die "Anatomie" der Formel hangeln.
Also: Auszurechnen ist
\(\frac{d}{dr} \left( r \left(\frac{du}{dr} + \nu \frac{u}{r} \right) \right) \)
Hier sollte erstmal die innere Klammer ausmultiplizieren, um den lästigen Quotienten u/r loszuwerden - die Quotienteregel ist nämlich relativ kompliziert:
\(\frac{d}{dr} \left( r \frac{du}{dr} + \nu u \right) \).
Konstante Faktoren kann man aus der Ableitung rausziehen, ebenso das "+". Dann hat man
\(\underbrace{\frac{d}{dr} \left( r \frac{du}{dr} \right)}_{A}+ \nu \frac{d}{dr} u \).
Nun auf A die Produktregel anwenden. Dann hat man:
\(\displaystyle \frac{dr}{dr} \frac{du}{dr} + r\frac{d}{dr}\frac{du}{dr} + \nu \frac{d}{dr}u \).
Nun noch alles ein bisschen schöner schreiben:
\(\displaystyle \frac{du}{dr} + r\frac{d^2u}{dr^2} + \nu \frac{du}{dr} \).
Ist also im Grunde genommen Schulstoff 11. Klasse, nur mit einer anderen Schreibweise.
Also: Auszurechnen ist
\(\frac{d}{dr} \left( r \left(\frac{du}{dr} + \nu \frac{u}{r} \right) \right) \)
Hier sollte erstmal die innere Klammer ausmultiplizieren, um den lästigen Quotienten u/r loszuwerden - die Quotienteregel ist nämlich relativ kompliziert:
\(\frac{d}{dr} \left( r \frac{du}{dr} + \nu u \right) \).
Konstante Faktoren kann man aus der Ableitung rausziehen, ebenso das "+". Dann hat man
\(\underbrace{\frac{d}{dr} \left( r \frac{du}{dr} \right)}_{A}+ \nu \frac{d}{dr} u \).
Nun auf A die Produktregel anwenden. Dann hat man:
\(\displaystyle \frac{dr}{dr} \frac{du}{dr} + r\frac{d}{dr}\frac{du}{dr} + \nu \frac{d}{dr}u \).
Nun noch alles ein bisschen schöner schreiben:
\(\displaystyle \frac{du}{dr} + r\frac{d^2u}{dr^2} + \nu \frac{du}{dr} \).
Ist also im Grunde genommen Schulstoff 11. Klasse, nur mit einer anderen Schreibweise.
Diese Antwort melden
Link
geantwortet

m.simon.539
Punkte: 2.37K
Punkte: 2.37K

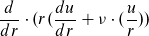
1. Ist das erste "\(\cdot\)" eine Multiplikation? Wenn ja, dann ist die Aufgabe trivial, und die Lösung ist kene Funktion, sondern ein Operator. Oder soll der Operator \(\frac{d}{dr}\) auf den nachfolgenden Term angewandt werden. Dann wäre das Ergebnis eine Funktion.
2. Ist das \(\nu\) konstant (also nicht von r abhängig)?
─ m.simon.539 21.02.2024 um 01:07