Dazu musst du im wesentlichen wissen wie die k-te Ableitung aussieht. Die ersten vier hast du ja schon, erkennst du das Muster? Der Nenner ist doch offensichtlich. Nun im Zähler: multiplizier mal nicht gleich aus, sondern lass die Faktoren stehen: erst 2, dann -2*2, dann -2*2*-2*2, dann... . -2*2*-2*2*3*2, wie geht's weiter?
Lehrer/Professor, Punkte: 38.93K
die Lösung soll (-1)^(k+1)*((2^k)/k) sein. Den ersten Teil verstehe ich, der ist dazu da das sich das Vorzeichen ändert, für k setze ich immer den Grad der Ableitung ein nur dann komme ich nicht auf die Lösungen die ich in Schritt 2 angegeben habe. ─ irukandji 17.10.2020 um 00:52
(-2)*2*(-2)*2*(-3)*2.........(-2)*2*(-2)*2*(-3)*2*(-4)*2.........(-2)*2*(-2)*2*(-3)*2*(-4)*2*(-5)*2 Also immer im Wechsel plus und Minus ─ irukandji 17.10.2020 um 14:32

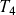 ,
, 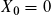
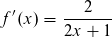
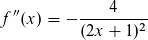
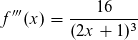
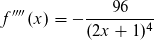
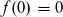
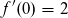
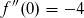
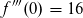
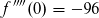
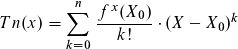
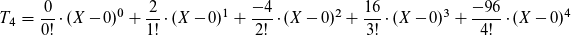
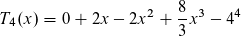
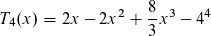
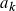 vor
vor 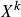 lautet.
lautet.