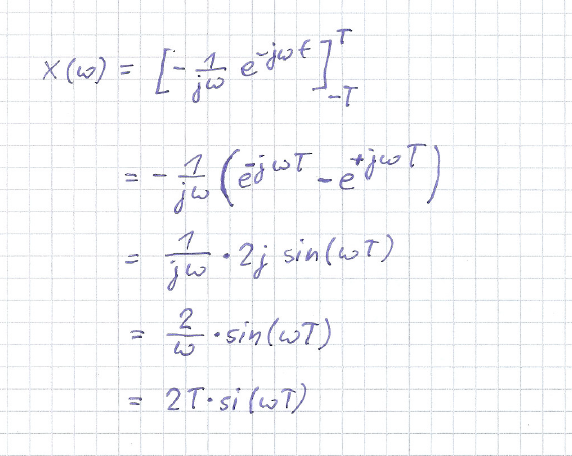Hallo,

undzwar verstehe ich nicht ganz wie man von der zweiten Zeile auf die dritte Zeile kommt. Ich weiß, dass der trigonometrische Funktion von Sinus verwendet wird, aber irgendwie macht, dass trotzdem nicht ganz Sinn für mich. Mich stört hierbei in der Klammer das Vorzeichen der Exponenten in der ersten e-Funktion. Für den Sinus Ansatz müsste dort doch eigentlich e^(jwT) - e^(-jwT) stehen, allerdings steht dort e^(-jwT) - e^(jwT) also genau andersherum. Auch die 2j die da auf einmal stehen kann ich nicht ganz nachvollziehen. Es bei dem Sinus Ansatz müsste dort doch 1/2j stehen.

Ich hoffe mein Verständnisproblem ist sichtbar.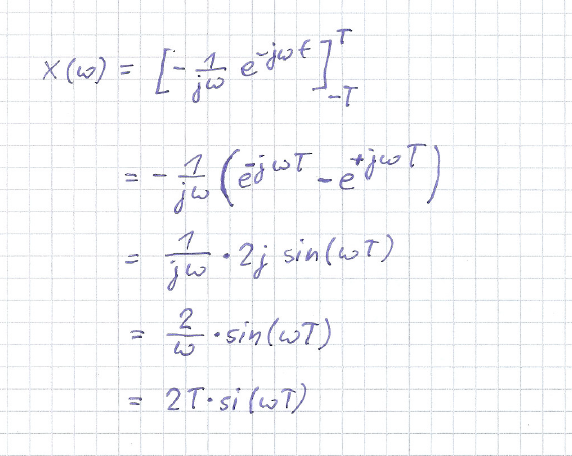
Ich glaube ich habs jetzt doch verstanden. Es wurden mehrere Schritte auf einmal gemacht, dass äußere Minus wurde in die Klammer gezogen und es wird umgestellt. Anschließend kann man ersetzen, allerdings sehe ich trotzdem nicht, wieso dort 2j anstatt 1/2j steht.