Moin,
ein Integral \(\int_{a}^{b}f(x)dx\),\(a\le b\) ist definiert als die (Netto-) Fläche unter dem Graphen von f(x) von a nach b. Also muss die markierte Fläche z.B. bei von -1 nach 2 gehen, das 3. Bilde fällt somit raus. Außerdem ist der Integrand, f(x), die Funktion, unter dessen Graphen die Fläche markiert ist, damit kannst du alle Bilder zuordnen.
LG

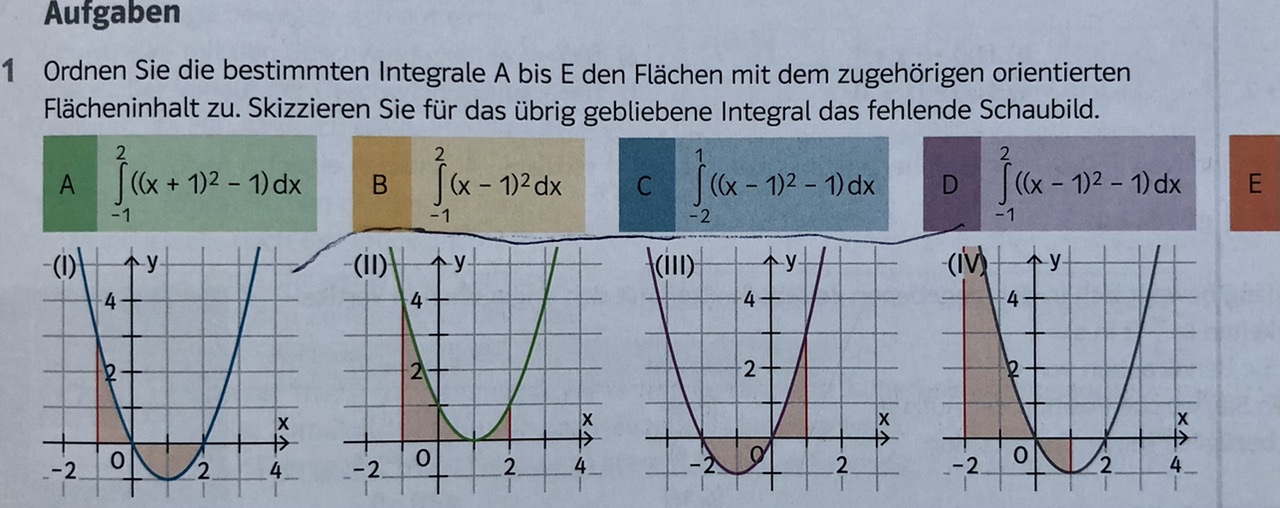
Zunächst kannst du anhand der Integralgrenzen unterscheiden. Das Flächeninhalt (der durch Graph und $x$-Achse begrenzt wird) muss nicht in Integrsl vorkommen. Du möchtest ja gerade diesen mit Hilfe des bestimmten Integral herausfinden.

Dann wird das Wissen über den Scheitelpunkt einer quadratischen Funktion benötigt. Wenn der Scheitelpunkt bei $S(d|e)$ liegt, dann lautet die zugehörige Scheitelpunktform der quadratischen Funktion $f(x)=a(x-d)^2+e$, wobei $a=1$ im Falle einer verschobenen Normalparabel ist (wie in deinen Beispielen auch). Wie du richtig erkannt hast verschiebt der Parameter $e$ die Funktion proportional entlang der $y$-Achse. Wie auch aus der Scheitelpunktform zu entnehmen ist, sorgt der Parameter $d$ dagegen für eine antiproportionale (umgekehrt proportional) Verschiebung entlang $x$-Achse. 

Mit diesen Hinweisen solltest du die Integrale den entsprechenden Visualisierungen zuordnen können, oder?