Folge, Grenzwert berechnen

Aufrufe: 837     Aktiv: 24.09.2019 um 10:55
0

Hallöchen liebe Community,

nachdem ich nun 2 Stunden versucht habe auf eine Lösung zu kommen, dachte ich, ich versuche mein Glück hier.

Meine Aufgabe ist letzlich den Grenzwert der unten gezeigten Folge (n gegen unendlich) zu berechnen. Ich nehme zwar auch gerne zusätzlich eine Komplettlösung, jedoch komme ich vermutlich nach dem Bilden des Hauptnenners von selbst weiter.

Ich habe versucht diesen selbst zu finden, indem ich zunächst mal den ersten Bruch auflöse (siehe Bild). Leider scheint das so wie ich es versucht habe nicht richtig zu sein. Kann mir jemand sagen, warum das nicht richtig ist und, wie ich stattdessen an den Hauptnenner komme?

Vielen Dank im Vorraus.

Diese Frage melden
gefragt

Student, Punkte: 10

 
Kommentar schreiben
1 Antwort
0

Ich kann nicht genau nachvollziehen, was du gemacht hast und deine zweite Zeile ist auch nicht äquivalent zur ersten!

Im Zweifel mach dir einfach wirklich die Mühe der Reihe nach alles auszumultiplizieren:

Wenn du das Glück hast und bei dieser recht unkreativen Methode am Schluss im Zähler und Nenner zwei Polynome mit dem gleichen führenden Grad stehen, kannst du den Grenzwert recht schnell an deren Koeffizienten ablesen.

Sollte der Grad nicht gleich sein, aber trotzdem schöne Standardpolynome im Zähler und Nenner, so kannst du schnell auf einen Grenzwert \(0\), \( \infty\), oder \( -\infty\) schließen.

 

Diese Antwort melden
geantwortet

Student, Punkte: 2.18K

 
Hallo,

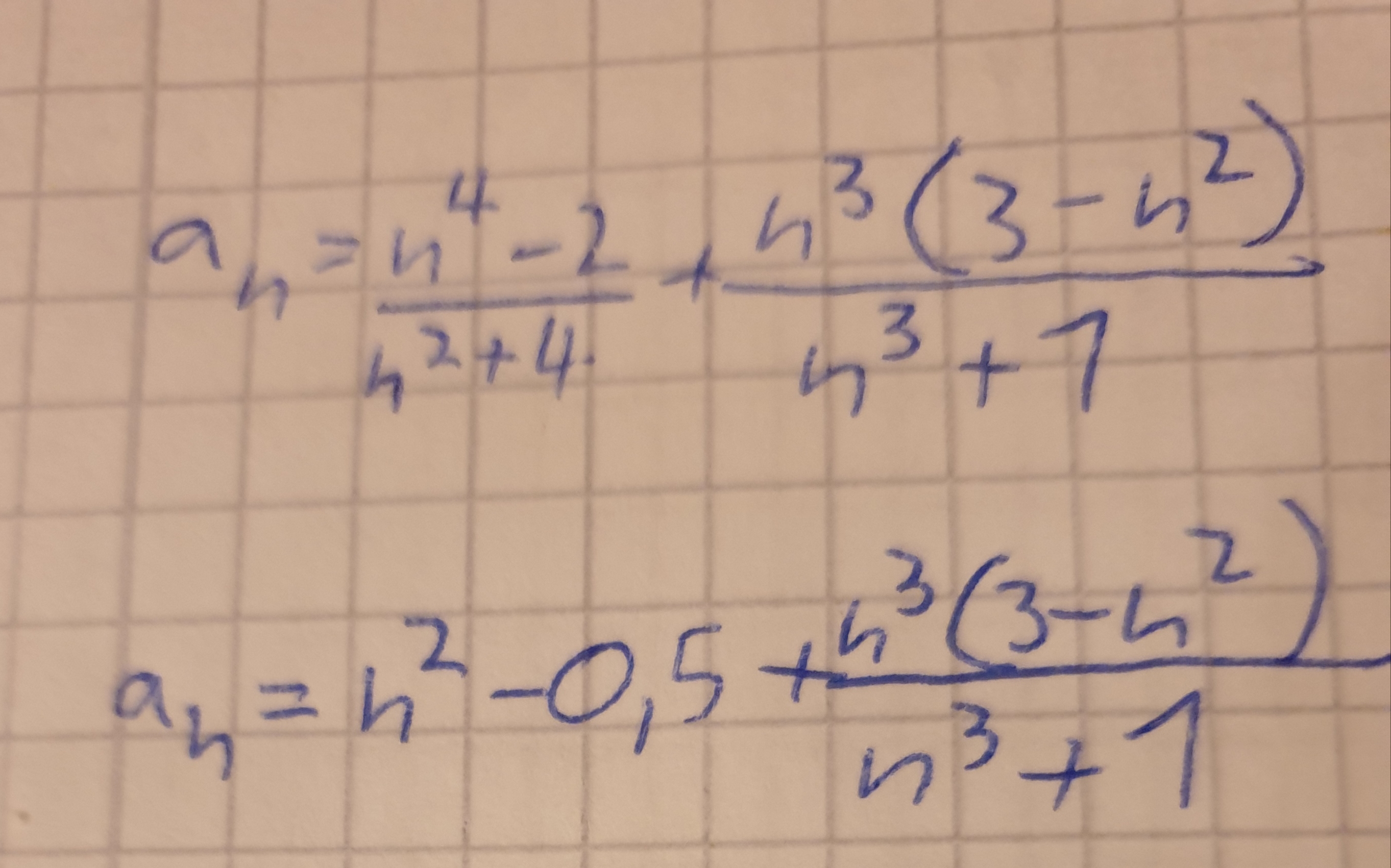
zunächst mal danke für das sehr aufwendige Rechenbeispiel! :)

Ich hatte keinen vernünftigen Ansatz gesehen und habe deswegen den ersten Bruch einfach geteilt. Die fehlende Äquivalenz ist mir dann auch aufgefallen. Auf diesem Weg kommt nämlich am Ende 2,5 raus. Da ich dann nicht weiter wusste, habe ich hier gefragt.

Deine Antwort ist sehr einleuchtend und verständlich. Danke sehr! :)   ─   fabsi 24.09.2019 um 10:49

Kommentar schreiben