1
Moin,
Ich versuch gerade die Konturlinien und den Gradienten zu meinem skalaren Feld:
$$f(x,y) = x^3 - 3xy^2$$
zu bestimmen. Bisher hab ich folgendes herausgefunden:
Ich habe Schwierigkeiten das in Verbindung mit dem kritischen Punkt zu bringen und irgendwas aussagekräftiges über meine Grafik zu sagen.
Außerdem: Wie komm ich denn auf den steilsten Aufstieg, sowie steilsten Abstieg?
Über Vorschläge wäre ich sehr dankbar.
Ich versuch gerade die Konturlinien und den Gradienten zu meinem skalaren Feld:
$$f(x,y) = x^3 - 3xy^2$$
zu bestimmen. Bisher hab ich folgendes herausgefunden:
Die Jakoby Matrix ist \(O \) wenn \( \frac{\partial f}{\partial x}= 3x^2 -3y^2 =0 \) und \( \frac{\partial f}{\partial y}=-6xy=0 \).
\(-6xy=0\) wenn \(x=0\) or \(y=0 \), und \(3x^2 -3y^2 =0\) falls \(x= \pm y\), also \(x=y=0\).
Deshalb ist \( (0,0) \) ein kritischer Punkt. Die Hesse Matrix gibt uns keine weiteren Informationen.
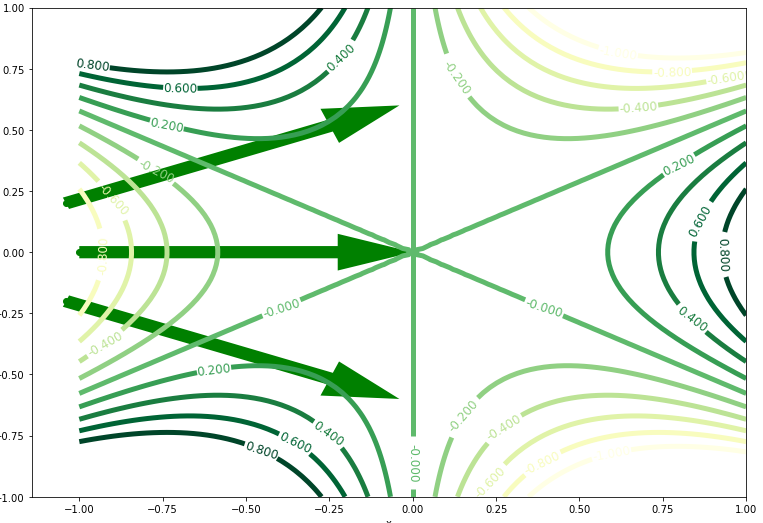
Nun habe ich versucht das skalare Feld mit Konturlinien darzustellen und es ist folgendes rausgekommen:
Nun habe ich versucht das skalare Feld mit Konturlinien darzustellen und es ist folgendes rausgekommen:

Ich habe Schwierigkeiten das in Verbindung mit dem kritischen Punkt zu bringen und irgendwas aussagekräftiges über meine Grafik zu sagen.
Außerdem: Wie komm ich denn auf den steilsten Aufstieg, sowie steilsten Abstieg?
Über Vorschläge wäre ich sehr dankbar.
Diese Frage melden
gefragt

inaktiver Nutzer
