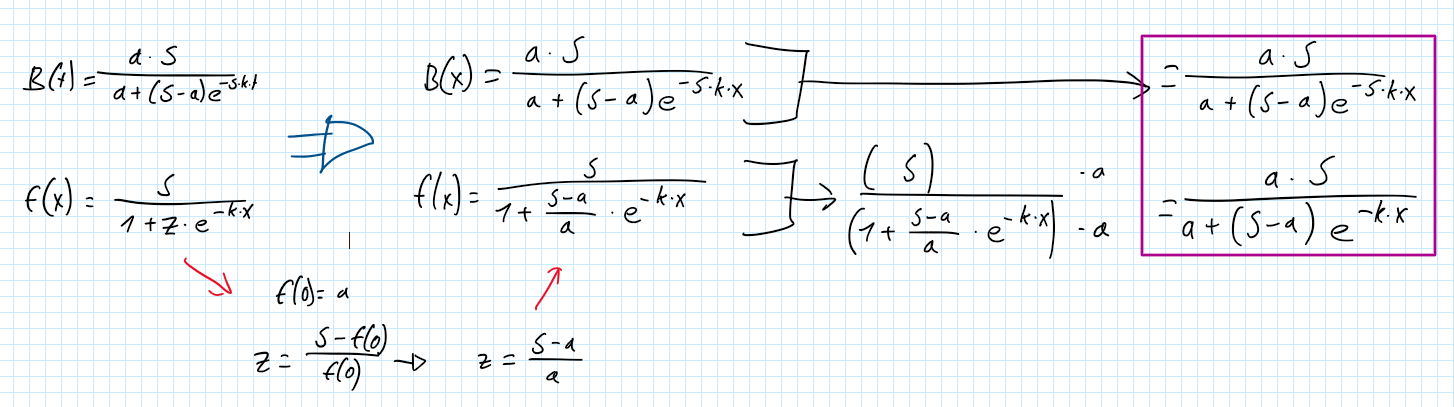Gibt es verschiedene Formeln für logistisches Wachstum?

Aufrufe: 405     Aktiv: 07.01.2022 um 23:46
0
Ich habe folgende Funktionen gefunden:

f(x) ist aus meinem Mathebuch und B(x) aus dem Internet (Quelle: https://www.schullv.de/mathe/basiswissen/analysis/wachstum/logistisches_wachstum)
Beide Quellen behaupten diese Formeln seien die Formeln für das Logistische Wachstum.

Wie man in dem Bild oben sieht habe ich versucht f(x) umzustellen um zu beweisen, dass beide Formeln im Prinzip das gleiche sind. 
Im lila Kasten ist leider unschwer zu erkennen, dass B(x) nicht gleich f(x) ist. 

Ein zusätzlicher Kontrollgang in Geogebra zeigt mir:

tatsächlich, die Funktionen sind nicht gleich. 

Nun zu meiner Frage:
Gibt es einfach mehrere Formeln und man sucht sich die aus die einem besser passt?
Wo liegt der Fehler? Vielleicht unterschiedlicher Anderwungsbereich? Keine Ahnung, ich komm nicht weiter. 

Bitte um Hilfe, Danke im Voraus
Diese Frage melden
gefragt

Schüler, Punkte: 12

 
Kommentar schreiben
2 Antworten
0
Bei $f(x)$ fehlt einfach nur das $S$ in der $\mathrm{e}$-Funktion. Das halte ich in dem Buch also eher für einen Druckfehler. Ansonsten wurde ja nur durch $a$ gekürzt.
Diese Antwort melden
geantwortet

Selbstständig, Punkte: 30.55K

 
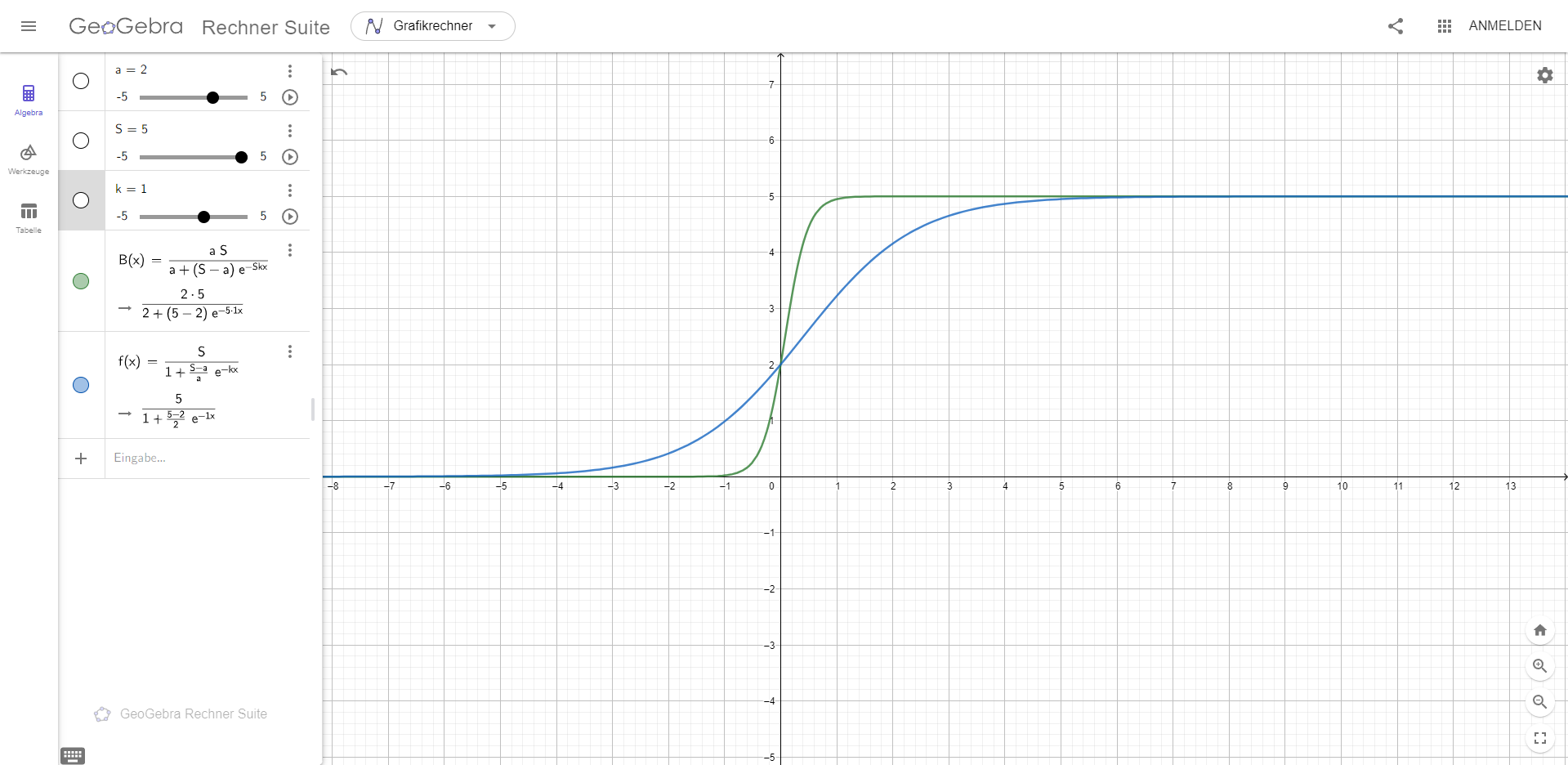
Einen Druckfehler kann ich eigentlich ausschließen, da sonst auf insgesamt 3 Seiten in über 10 Fällen solch ein Druckfehler wäre.   ─   marc.yeee 07.01.2022 um 21:28

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Cauchy wurde bereits informiert.
0
Natürlich ist $f(x)\neq B(x)$, aber die Funktionenklasse ist die gleiche. Ein Teil der Umbenennungen hast Du ja gefunden, $z:=\frac{S-a}a$. Und dann in $f$ noch $k_f=S\cdot k_B$ setzen, dann sieht man: die Funktionentypen sind identisch. Die Werte von $f$ werden auch von $g$ angenommen, nur an anderen Stellen $x$.
Genauer: Mit $z$ wie oben definiert ist und $k=k_B$ ist $f(x)=B(Sx)$. D.h. $f$ unterscheidet sich von $B$ nur in einer Skalierung auf der $x$-Achse.
Diese Antwort melden
geantwortet

Lehrer/Professor, Punkte: 38.88K

 

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Mikn wurde bereits informiert.