Die Ableitung der Funktion h(t) lässt sich unkompliziert bilden!
Zuerst benutzt du die Summenregel: Bei einer endlichen Summe von Funktionen darf gliedweise differenziert werden.
Das heißt in deinem Beispiel, dass du um h(t) abzuleiten dieses zerlegst in:
\( h(t) =h_{1}(t)+ h_{2}(t)+h_{3}(t)+h_{4}(t) \)
mit
\( h_{1}(t) =\frac{97}{1372500}t^{3} \)
\( h_{2}(t) =- \frac{23197}{1372500}t^{2} \)
\( h_{3}(t) = 2\frac{874}{2745}t \)
\( h_{4}(t) =-9\frac{275}{549} \)
(falls ich irgendwelche Ziffern falsch abgetippt habe ignorier es einfach, das macht für die Ableitung keinen Unterschied, wenn du dann die richtigen Ziffern benutzt)
Die Summenregel besagt jetzt eben, dass wir unsere einzelnen \( h_{...}(t) \) einzeln Ableiten können und deren Summe dann die Ableitung von h(t) ist. Also machen wir uns Gedanken, wie wir diese ableiten können.
Sie haben alle die Form \( h_{...}(t) = c\cdot t^{k} \) also einen Konstanten Faktor und eine Potenz von deiner Variable t.
In deinen Unterlagen findest du bestimmt wie man diese einzelnen Summanden ableiten kann, das ist die Standardregel:
\( f(x)=c \cdot x^{k} \quad \Rightarrow \quad f'(x) = k\cdot c\cdot x^{k-1} \)
Also zum Beispiel für deinen ersten Summanden:
\( h_{1}(t) = \frac{97}{1372500}t^{3} \quad \Rightarrow \quad h_{1}'(t)=3 \cdot \frac{97}{1372500} t^{2} \)
Versuche doch mal die anderen allein, vielleicht kannst du jetzt sogar die ganze Aufgabe lösen.
Student, Punkte: 2.18K

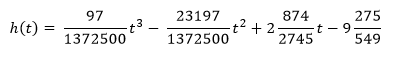 beschrieben werden.
beschrieben werden.
─ jojoliese 30.11.2020 um 10:08