0
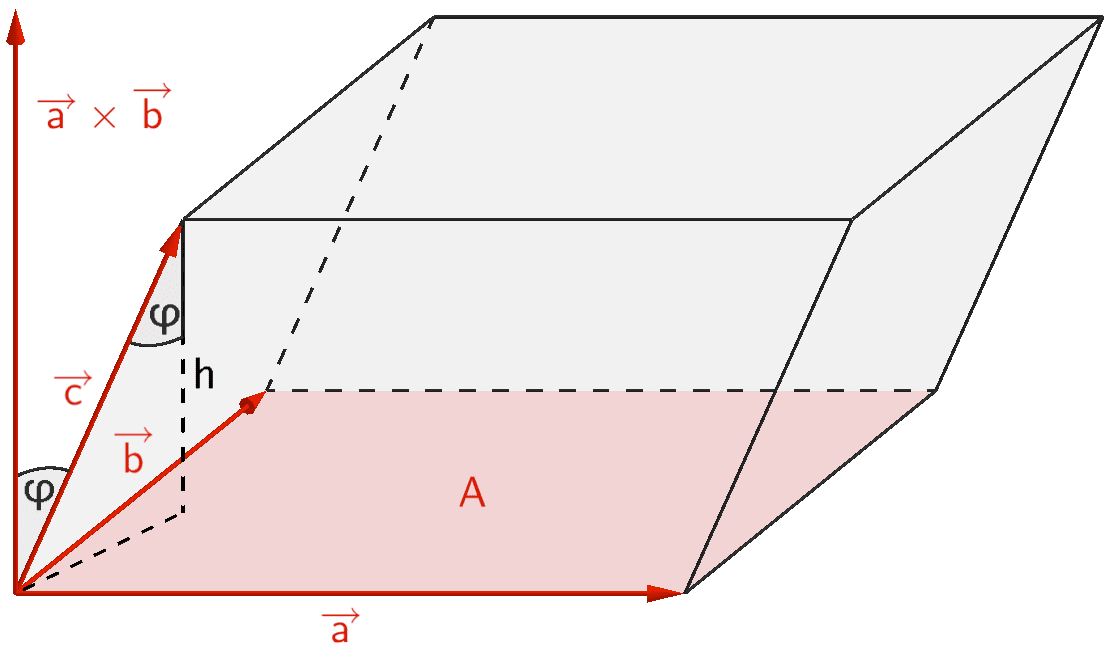
Sagen wir mal, wir wollen eine Formel mit \(\vec a,\vec b,\vec c\) für das Volumen \(V\) eines Spats herleiten. Es gilt mit den Notationen aus dem Bild \(V=Ah\) und \(A=|\vec a\times\vec b|\), das hast du ja auch schon erkannt. Weiter gilt \(h=|\vec c|\cdot\cos\varphi\) (verwende die Definition des Kosinus in dem gestrichelten rechtwinkligen Dreieck). Folglich ergibt sich \(V=|\vec a\times\vec b|\cdot|\vec c|\cdot\cos\varphi\). Nun ist \(\varphi\) aber auch der Winkel zwischen \(\vec a\times\vec b\) und \(\vec c\), wie es auch in der Graphik eingezeichnet ist, denn die beiden eingezeichneten Winkel sind Wechselwinkel zueinander. Ausdrücke der Form \(|\text{Vektor}|\cdot|\text{Vektor}|\cdot\cos(\text{Winkel zwischen den Vektoren})\) sollten dir bekannt vorkommen, das ist genau das Skalarprodukt. Also ergibt sich \(V=(\vec a\times\vec b)\circ\vec c\). Hier bilden \(\vec a,\vec b,\vec c\) ein Rechtssystem, wäre die Orientierung anders, dann käme ein \(-1\) dazu, deshalb braucht man im Allgemeinen noch einen Betrag.
Diese Antwort melden
Link
geantwortet

stal
Punkte: 11.27K
Punkte: 11.27K
