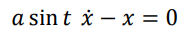\[    a\sin(t)\frac{dx}{dt} -x = 0 \Leftrightarrow  a\sin(t)\frac{dx}{dt} = x \\ \Leftrightarrow a\sin(t)dx = xdt \Leftrightarrow  \frac{dx}{x}= \frac{dt}{a\sin(t)} = \frac{1}{a}\csc(t) dt \\ \Leftrightarrow \int \frac{dx}{x} = \int \frac{1}{a}\csc(t) dt \Leftrightarrow ln|x| + C = \frac{1}{a} \int \csc(t) \cdot \frac{csc(t)-cot(t)}{csc(t)-cot(t)} dt \\ \Leftrightarrow ln|x| + C = \frac{1}{a} \int \frac{(csc^2(t)-cot(t)csc(t))dt}{csc(t)-cot(t)} \]

Sei nun \( u=csc(t)-cot(t) \Rightarrow \frac{du}{dt}=(-cot(t)csc(t)-(-csc^2(t))) \Rightarrow du=(csc^2(t)-cot(t)csc(t))dt \)

\[ \Rightarrow ln|x| + C = \frac{1}{a} \int \frac{(csc^2(t)-cot(t)csc(t))dt}{csc(t)-cot(t)} \\ \Leftrightarrow ln|x| + C = \frac{1}{a} \int \frac{du}{u} \\ \Leftrightarrow ln|x| + C = \frac{1}{a}ln|u| = \frac{1}{a}ln|csc(t)-cot(t)| \\ \Leftrightarrow e^{ln|x| + C} = e^{\frac{1}{a}ln|csc(t)-cot(t)|} \\ \Leftrightarrow Kx = (csc(t)-cot(t))^{\frac{1}{a}} \\ \Leftrightarrow x(t) = k \sqrt[a]{csc(t)-cot(t)} \]

Der Ansatz Trennung der Variablen führt auf

\[\frac{\mathrm{d}x}x = \frac{\mathrm{d}t}{a \sin t}\]

Ich weiß aber nicht, wie man die rechte Seite integriert.

Der Begriff der Stammfunkttion ist ein Synonym für unbestimmtes Integral, was völlig verschieden gegenüber dem bestimmten Integral ist, dass als Grenzwert von ober- und Untersumme definiert ist. Über den Hauptsatz der Differenzial- und Integralrechnung wird aber ein Zusammenhang zwischen beiden Bildungen hergestellt. Das ist nicht nur meine Meinung, sondern wohl allgemein richtig. Genauer habe ich das in meinen Videos zur Integralrechnung dargelegt.

Falls es jemand nicht lesen kann. Bei mir ist es komischerweise schon kompiliert.