Warum kann ich bei einem ein Integral bilden und beim anderen nicht für die Flächenberechnung?

Erste Frage Aufrufe: 382     Aktiv: 16.05.2021 um 21:48
0
Hallo, ich bin gerade am verzweifeln. Ich habe zwei aufgaben erhalten. Wo ich jeweils zwei Funktionen habe, immer eine Gerade und eine anderere Funktion. Beides mal soll ich den Flächeninhalt berechnen.

Aufgabe 1:
Hier bei dem kommenden Schaubild soll ich die Flächevon 0 bis -2 berechnen. Ich kann jetzt hier einfach ein Integral von -2 bis 0 bilden und muss einfach die obere Funktion minus der Funktion der Geraden rechnen und erhalte mein Ergebnis.



2.Aufgabe

Bei der zweiten Aufgabe habe ich wieder zwei Funktionen, erneut eine Gerade und eine andere Funktion halt. Ich soll die schraffierte Fläche berechnen. Nun dachte ich mir, dass ich das gleich wie oben machen kann, in dem ich einfach ein Integral von 0 bis 2 bilde und dann einfach eine Funktion von der anderen abziehe, aber hier geht das nicht so warum und wie erkenne ich, dass ich das jetzt nicht so machen darf?




Ich habe den Lösungsweg nachvollziehen können, wie ich bei dem 2 Schaubild nun die Fläche berechne, aebr wie kann ich erkennen, dass ich jetzt hier kein Integral bilden darf, sondern diesen anderen Lösungsweg nutzen muss? Also warum geht das jetzt nicht mehr, mit dem Lösungsweg, dass ich ein Integral bilde und die die Differenz der Funktionen ziehe? WIe kann man erkennen, dass das nicht mehr möglich ist?
Diese Frage melden
gefragt

Punkte: 16

 
Kommentar schreiben
2 Antworten
0
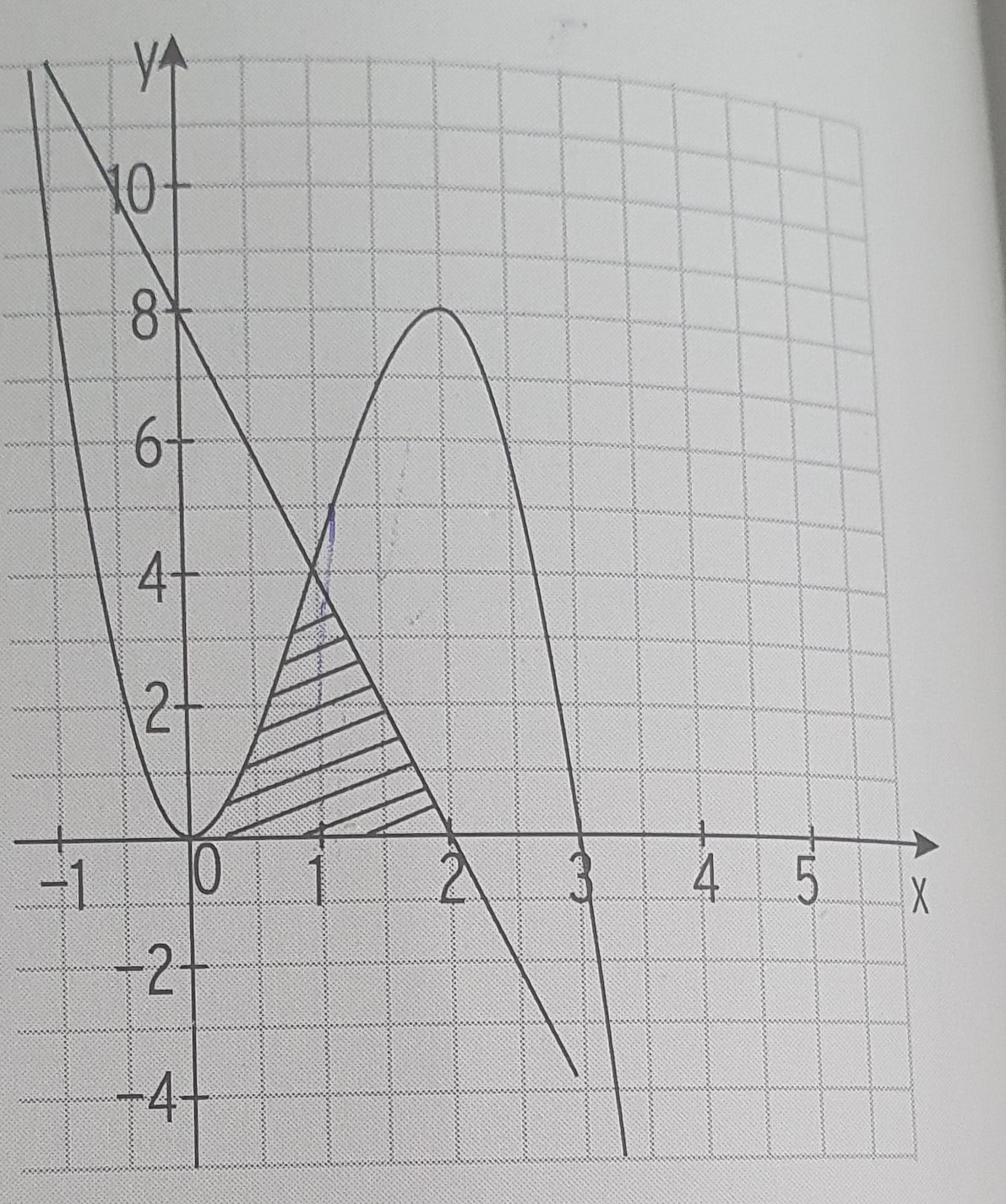
Das käme heraus, wenn du die Fläche mittels Integral von 0 bis 2 berechnen würdest. Ohne Wechsel der oberen und unteren Funktion an der Schnittstelle, hätten beide Flächen unterschiedliche VZ und würden miteinander verrechnet werden.
Diese Antwort melden
geantwortet

selbstständig, Punkte: 11.89K

 

Kommentar schreiben

0
Beim zweiten Schaubild hat man keine Fläche zwischen den Funktionen, sondern zwischen jeweils einer der Funktionen und der \(x\)-Achse. Daher hilft dir die Differenz der Funktionen hier nicht.
Diese Antwort melden
geantwortet

Selbstständig, Punkte: 30.55K

 
Danke, nur habe ich das leider nicht ganz verstanden :(. Wenn jetzt beispielsweise beim ersten Schaubild die Gerade z.B durch -1 verlaufen würde, also die X-Achse bei -1 schneiden würde, hätte ich ja auch eine Fläche zwischen der x-Achse, wäre dann die Differenz auch nicht mehr möglich?   ─   ichbinlost 16.05.2021 um 14:52
Okay danke, also könnte ich theoretisch gesehen, beim zweiten Schaubild die Fläche zwischen 0 und 1 rehcnen, dass würde passen oder?   ─   ichbinlost 16.05.2021 um 15:08

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Cauchy wurde bereits informiert.