Hi,

4.54 a) hierzu kannst du die Stammfunktion F(t) nutzen und dann F(3) - F(0,5) berechnen. Damit hast du die Fläche unter dem Graphen von 0,5 bis 3.

Allerdings muss davon noch die Fläche von 0,5 bis zur Schnittstelle von f(x) und y=2 über y=2 abgezogen werden. Am besten zeichnest du dir das mal auf.

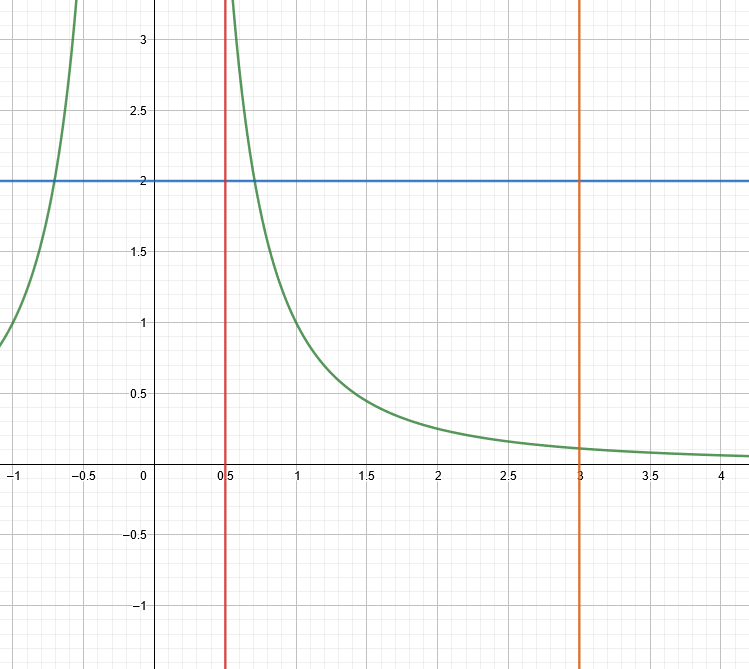
Du möchtest die Fläche unter dem Graphen von 0,5 bis 3 berechnen, aber laut Aufgabenstellung soll die Fläche oberhalb y=2 nicht mitgerechnet werden.
Ansatz etwas umgeändert aber ist glaube ich einfacher:

Wir berechnen erstmal den Schnittpunkt von f(t) mit y=2. (Auf dem Bild der Schnittpunkt von der blauen und grünen Linie im positiven Bereich)
Dann berechnen wir das Integral von diesem Schnittpunkt bis 3, also die Fläche unter dem Graphen in diesem Intervall.
Danach müssen wir noch die Fläche von 0.5 bis zu dem Schnittpunkt berechnen.

Fangen wir erstmal an den Schnittpunkt zu berechnen.

Also: wann nimmt die Funktion den Wert 2 an?
Schnittpunkt f(t) mit y=2 bestimmen:
\(
f(t) = 2 \\
\frac{1}{t^{2}} = 2
\Rightarrow t = \frac{1}{\sqrt{2}}
\)

Berechne das Intervall von \(\frac{1}{\sqrt{2}}\) bis 3 mit der Stammfunktion F(t):
(hierbei wird F(3) von F(\(\frac{1}{\sqrt{2}}\)) abgezogen, da der Graph im angegebenen Intervall fällt)
\(
F(t) = -\frac{1}{t} \\
F(\frac{1}{\sqrt{2}}) - F(3)=  (-\frac{1}{\sqrt{2}}) - (-\frac{1}{3}) = -1,08 (ca.)  \\
\)
Wir betrachten die Fläche, also 1,08.
Plus die Fläche von 0,5 bis \(\frac{1}{\sqrt{2}}\), die jetzt ein Rechteck ist durch y = 2:
\(
\frac{1}{\sqrt{2}} - 0,5 = 0,2071\\

0,2071 * 2 = 0,414\\

1,08 + 0,414 = 1,49
\)

Ich habe teilweise gerundet, deswegen ist das Ergebnis nicht 100% exakt.
Aber die Fläche unter dem Graphen ist also etwa 1,49 Flächeneinheiten groß.

Hoffe das ist so verständlich :)