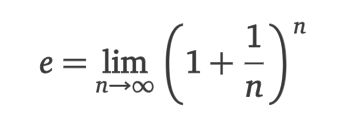1
Herzlich Willkommen auf mathefragen.de! Du hast sicherlich den Fehler gemacht "teilweise" den Grenzwert zu nehmen, indem du erst $\frac{1}{n}$ für $n\longrightarrow \infty$ gegen Null laufen lässt und dann den Grenzwert von $1^n$ betrachtest. Dieses Vorgehen den Limes "teilweise" zu nehmen bitte garnicht erst angewöhnen.
Du kannst die Folgeglieder ja einmal für $n=1,2,3,\ldots$ ausrechnen. Dann wirst du sehen das sich die Folgelieder nicht immer näher zu 1 sondern gegen einen anderen Wert ($e$) laufen, also von $1$ weg. Die Erklärung warum es ausgerechnet gegen die Eulersche Zahl läuft hängt etwas davon ab ob du Schüler (wie bei dir im Profil beschrieben) oder Student bist?
Du kannst die Folgeglieder ja einmal für $n=1,2,3,\ldots$ ausrechnen. Dann wirst du sehen das sich die Folgelieder nicht immer näher zu 1 sondern gegen einen anderen Wert ($e$) laufen, also von $1$ weg. Die Erklärung warum es ausgerechnet gegen die Eulersche Zahl läuft hängt etwas davon ab ob du Schüler (wie bei dir im Profil beschrieben) oder Student bist?
Diese Antwort melden
Link
geantwortet

maqu
Punkte: 8.84K
Punkte: 8.84K
Schüler
─
brightphoenix
23.04.2022 um 15:11
Ok ich versuche das mal schülergerecht zu erklären. Ich nehme an ihr habt Folgen im Unterricht ein wenig behandelt und auch über Monotonie und Beschränktheit gesprochen. Ob ihr Grenzwertsätze behandelt habt weiß ich jetzt nicht, das hängt vom Lernplan des jeweiligen Bundeslandes ab. In einigen Bundesländern werden Folgen sogar garnicht mehr behandelt.
Zuerst sollte man sich überlegen, dass $\underset{n\longrightarrow \infty}{\lim} \left(1+\frac{1}{n}\right)^n=g$ gilt, also die Folge erstmal überhaupt einen Grenzwert besitzt.
Man betrachte dazu die Folgen $a_n=\left(1+\frac{1}{n}\right)^n$ und $b_n=\left(1+\frac{1}{n}\right)^{n+1}$. Durch einsetzen von verschiedenen Werten für $n$ kann man erkennen, dass $a_n$ monoton wachsend ist und $b_n$ monoton fallend. Weiterhin gilt stets $a_n < b_n$ für alle natürlichen Zahlen $n$. Also sind sowohl $a_n$ als auch $b_n$ nach unten durch $a_1$ beschränkt und nach oben durch $b_1$. Wärst du Student müsstest du diese Eigenschaften genau begründen, aber als Schüler reicht es denke ich aus, dass du diese Eigenschaften durch einsetzen für $n=1,2,3,4,\ldots$ ermitteln kannst. Nun ist dir vielleicht bekannt das eine Folge genau dann konvergiert (einen Grenzwert besitzt) wenn sie monoton (wachsend/fallend) und beschränkt (oben/unten) ist. Somit gelten also $\underset{n\longrightarrow \infty}{\lim} a_n=g_1$ und $\underset{n\longrightarrow \infty}{\lim} b_n=g_2$. D.h., beide Folgen besitzen einen Grenzwert.
Nun kann man entweder mit Hilfe der Grenzwertsätze einfach zeigen, dass $\underset{n\longrightarrow \infty}{\lim} a_n=\underset{n\longrightarrow \infty}{\lim} b_n$ gilt, also beide den gleichen Grenzwert haben. Solltet ihr diese nicht besprochen haben, würde ich vorschlagen eine Annäherung an den Grenzwert beider Folgen zu machen (für $n$ große Zahlen einzusetzen). Da erkennt man dann nämlich auch, dass sich die Folge der eulerschen Zahl $e$ ännähert.
Unter folgendem Link ist dies nochmal anhand einer Annäherungstabelle dargestellt. https://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/eulersche-zahl#
Ich hoffe es wird so nun etwas deutlicher für dich. ─ maqu 24.04.2022 um 10:00
Zuerst sollte man sich überlegen, dass $\underset{n\longrightarrow \infty}{\lim} \left(1+\frac{1}{n}\right)^n=g$ gilt, also die Folge erstmal überhaupt einen Grenzwert besitzt.
Man betrachte dazu die Folgen $a_n=\left(1+\frac{1}{n}\right)^n$ und $b_n=\left(1+\frac{1}{n}\right)^{n+1}$. Durch einsetzen von verschiedenen Werten für $n$ kann man erkennen, dass $a_n$ monoton wachsend ist und $b_n$ monoton fallend. Weiterhin gilt stets $a_n < b_n$ für alle natürlichen Zahlen $n$. Also sind sowohl $a_n$ als auch $b_n$ nach unten durch $a_1$ beschränkt und nach oben durch $b_1$. Wärst du Student müsstest du diese Eigenschaften genau begründen, aber als Schüler reicht es denke ich aus, dass du diese Eigenschaften durch einsetzen für $n=1,2,3,4,\ldots$ ermitteln kannst. Nun ist dir vielleicht bekannt das eine Folge genau dann konvergiert (einen Grenzwert besitzt) wenn sie monoton (wachsend/fallend) und beschränkt (oben/unten) ist. Somit gelten also $\underset{n\longrightarrow \infty}{\lim} a_n=g_1$ und $\underset{n\longrightarrow \infty}{\lim} b_n=g_2$. D.h., beide Folgen besitzen einen Grenzwert.
Nun kann man entweder mit Hilfe der Grenzwertsätze einfach zeigen, dass $\underset{n\longrightarrow \infty}{\lim} a_n=\underset{n\longrightarrow \infty}{\lim} b_n$ gilt, also beide den gleichen Grenzwert haben. Solltet ihr diese nicht besprochen haben, würde ich vorschlagen eine Annäherung an den Grenzwert beider Folgen zu machen (für $n$ große Zahlen einzusetzen). Da erkennt man dann nämlich auch, dass sich die Folge der eulerschen Zahl $e$ ännähert.
Unter folgendem Link ist dies nochmal anhand einer Annäherungstabelle dargestellt. https://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/eulersche-zahl#
Ich hoffe es wird so nun etwas deutlicher für dich. ─ maqu 24.04.2022 um 10:00
Vielen Dank!
─
brightphoenix
24.04.2022 um 12:33