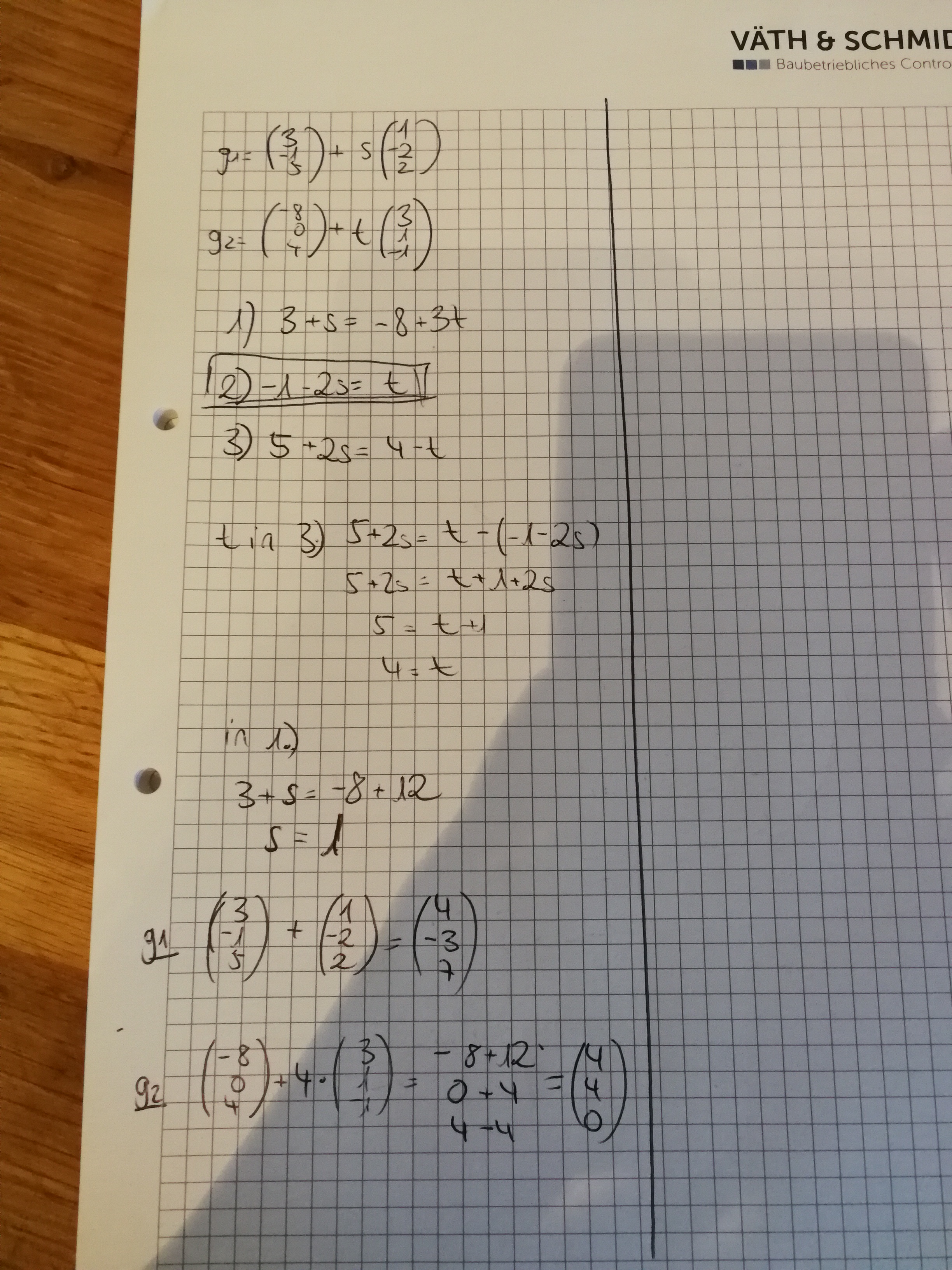Schnittpunkt von Geraden mit Variable R

Erste Frage Aufrufe: 781     Aktiv: 22.11.2021 um 22:04
0

Hallo,
ich sitze an einer Aufgabe zum Schnittpunkt zweier Geraden, bei der ich nicht weiter komme.

Die Aufgabe lautet:
Seien g1 und g2 Geraden, die sich in einem Punkt S Element R^3 schneiden. Bestimmen Sie S. Die Koordinaten von S sind alle ganzzahlig.

g1= (3;-1;5)+R*(1;-2;2)
g2= (-8;0;4)+R*(3;1;-1)

Das R ist die Menge der reellen Zahlen. Und das ist auch der Punkt, der mich am meisten verwirrt. Wenn ich ein Gleichungssystem aufstelle und nach R auflöse, erhalte ich R=-1/3 und damit den Schnittpunkt (-9;-1/3;13/3). Aber das darf ja durch die Bedingung dass alle Koordinaten von S ganzzahlig sein sollen, nicht sein. Ich habe auch versucht, R durch s und t zu ersetzen, also zwei verschiedene Variablen für die Geraden zu wählen, aber da erhält man dann zwei unterschiedliche Schnittpunkte. 

Ich hoffe sehr, dass mir jemand hier helfen kann und mir vielleicht auch erklären kann, was das mit der Variablen der Menge R bedeuten soll.

Außerdem sollte ich vielleicht erwähnen, dass ich noch nicht oft mathematische Ausdrücke in den Computer getippt habe, deshalb entschuldige ich mich für die vielleicht komische Darstellung. Ich habe einfach auch keine Ahnung wie man mathematische Ausdrücke vernünftig tippt.

Vielen Dank im Voraus allen die vielleicht helfen können!

Liebe Grüße

Evelyn

EDIT vom 21.11.2021 um 10:51:


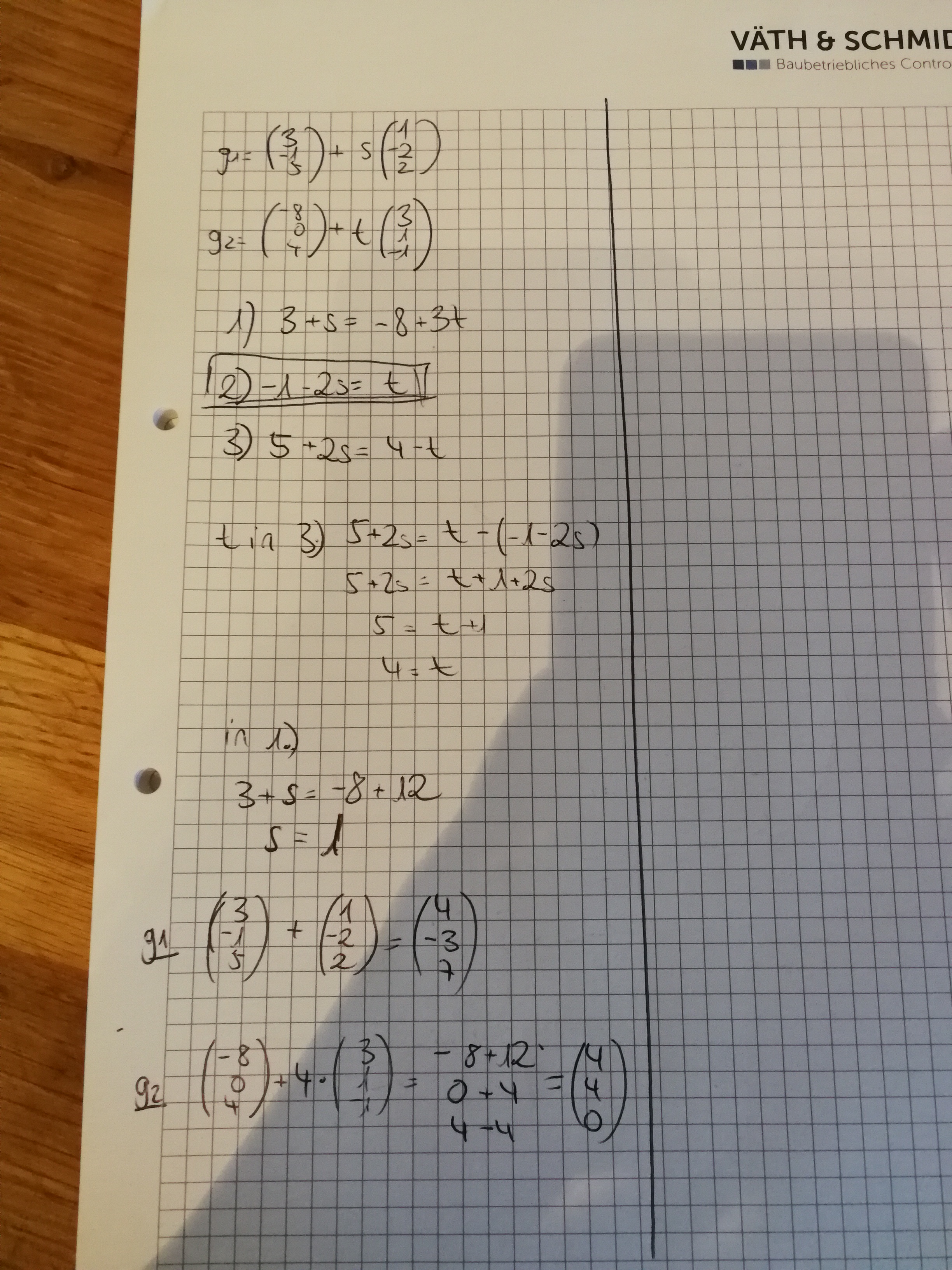
hier ist noch das Foto meiner Rechnung, gestern hatte das Hochladen wohl nicht funktioniert.
Diese Frage melden
gefragt

Student, Punkte: 12

 
Kommentar schreiben
1 Antwort
1
Wo auch immer du diese Schreibweise mit dem R her hast... das ist so völlig unüblich. In der Regel stehen da wirklich Parameter $s$ und $t$, die dann tatsächlich auch beide aus den reellen Zahlen sind, das schreibt man dann aber $s,t\in\mathbb{R}$. 

Warum du zwei unterschiedliche Schnittpunkte herausbekommst, ist ohne deine konkrete Rechnung schwer zu sagen. Ich vermute, dass du dich irgendwo verrechnet hast. Daher wäre es hilfreich, wenn du deine Rechnung einmal als Bild hochlädst.
Diese Antwort melden
geantwortet

Selbstständig, Punkte: 30.55K

 
Danke für die schnelle Antwort! Mir kam das auch unüblich vor, aber so war die Aufgabenstellung der Hausübung für die Uni... Ich schicke gleich mal ein Foto :)   ─   elevyn 20.11.2021 um 08:01
Ich habe diese Schreibweise schon oft gesehen: \(\mathbb{R}v:=\{\lambda v|\lambda \in \mathbb{R}\}\) Diese Schreibweise hat den Vorteil, dass man ganz einfach eine Menge aufachreiben kann, z.B. \(\mathrm{span}_K(v_1,\ldots,v_n)=\sum_{i=1}^n Kv_i\). Ansonsten müsste man ja streng genommen auch immer Mengenklammern bei affinen Mengen (Geraden, Ebenen,...) setzen   ─   mathejean 20.11.2021 um 09:29
Dankeschön für die Info mathejean, das ist gut zu wissen. Aber wie rechne ich das dann?
   ─   elevyn 21.11.2021 um 10:52
Streng formal ist deine Gerade jetzt eine affine Menge (sogar ein affiner UVR) und mit Mengen kann man ja so gar nicht rechnen wie mit Gleichungen. Man betrachtet deshalb eine Parameterisierung \(\Phi\), hier von der Form \(\mathbb{R}\to \mathbb{R}^3\). Wenn sowas aber nicht besprochen wurde (wird es eigentlich nie in Anfängervorlesungen), machst du das einfach wie "gewohnt". Vielleicht bietet sich hier auch eine Diskussion im Tutorium an.   ─   mathejean 21.11.2021 um 11:33
Dankeschön :)
   ─   elevyn 22.11.2021 um 21:55

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Cauchy wurde bereits informiert.