1
Hallo,
du beschreibst doch in deinem Titel bereits, dass die Ableitung für die Steigung steht.
Stell dir doch mal vor du gehst dem Graphen entlang, so als würdest du einen Berg besteigen.
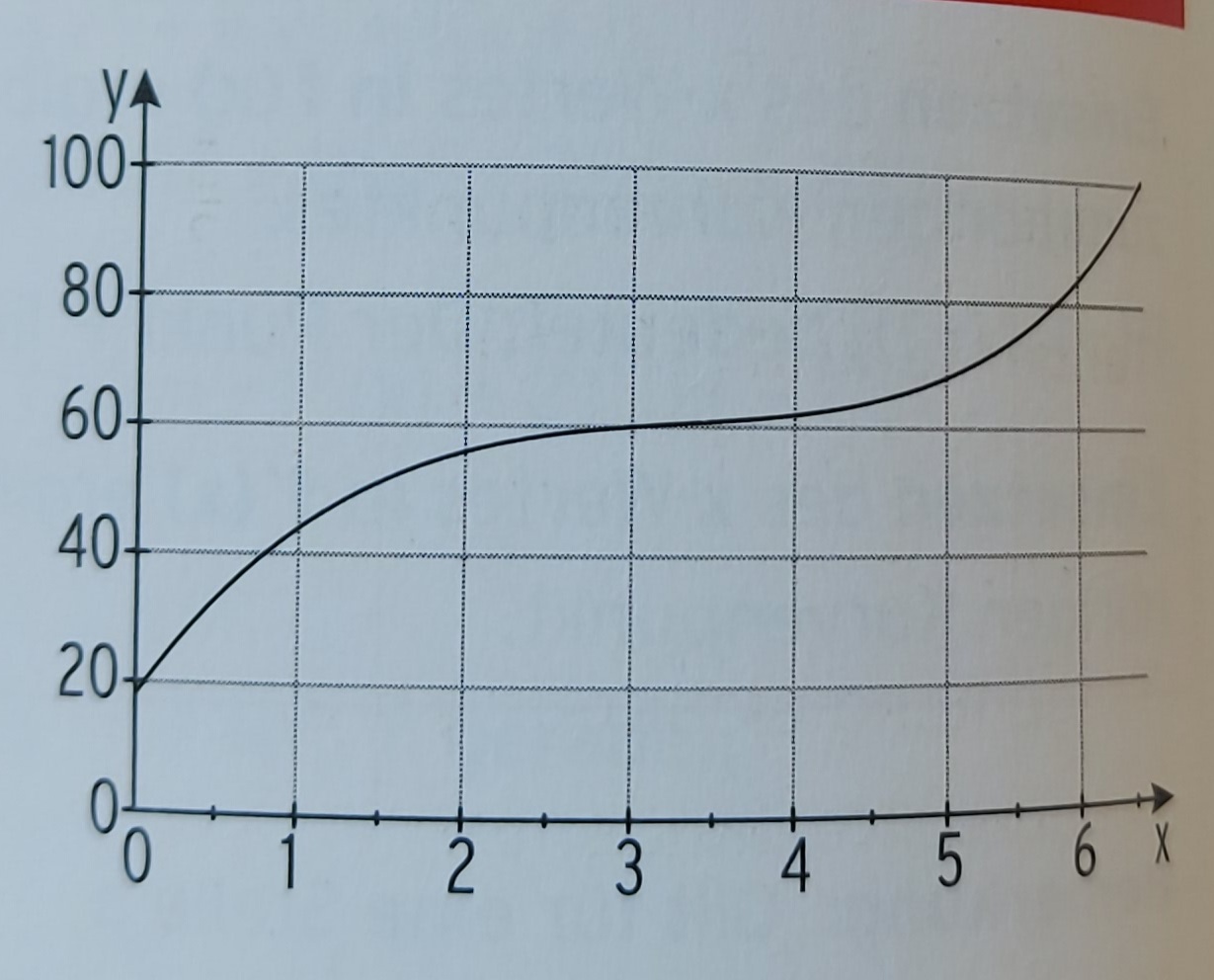
Ist der Anstieg bei $x=1$ oder bei $x=2$ steiler?
Gehst du bei $x=4$ den Berg runter oder hoch?
Versuch mal selbst in Worte zu fassen, wass $f'(x) >0$ für $1\leq x \leq 6$ bedeutet.
Grüße Christian
du beschreibst doch in deinem Titel bereits, dass die Ableitung für die Steigung steht.
Stell dir doch mal vor du gehst dem Graphen entlang, so als würdest du einen Berg besteigen.
Ist der Anstieg bei $x=1$ oder bei $x=2$ steiler?
Gehst du bei $x=4$ den Berg runter oder hoch?
Versuch mal selbst in Worte zu fassen, wass $f'(x) >0$ für $1\leq x \leq 6$ bedeutet.
Grüße Christian
Diese Antwort melden
Link
geantwortet

christian_strack
Sonstiger Berufsstatus, Punkte: 29.81K
Sonstiger Berufsstatus, Punkte: 29.81K