Ein Vergleich beider Methoden scheint nicht sinnvoll. Schon gar nicht, falls das Deine Idee ist, irgendeine Merkregel herzuleiten.
Lehrer/Professor, Punkte: 39.63K
Daher wollte ich nachfragen. Ich habe dir mal das Beispiel gezeichent, daher wollte ich fragen, bei der cramerischen Regel, wenn ich z. B. bei A_1 die Stelle i_(1,2) betrachte, ich streiche die 1 Spalte und zweite Zeile durch und nehme dann die Werte oder? Und bei i_(1,3) Streiche ich die erste Spalte und 3 Zeile?
Und bei Laplace wenn ich z. B. bei i_(1,2) bin, streiche ich die 1 Zeile und 2 Spalte und betrachte die Werte oder? ─ user465529 10.01.2023 um 00:07


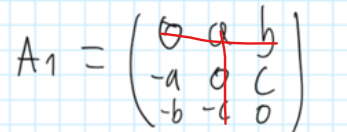
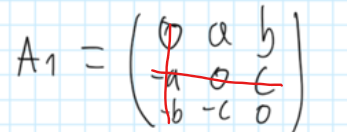
Sehe ich jedoch und wie es aussieht Du auch, nicht so.
Habe ich das richtig interpretiert? Also wie es bei Laplace und wie es bei Cramersch ist, für die Stelle i_(1,2)? ─ user465529 09.01.2023 um 20:19