1
= -3/8cos(3x)*cos(x)-1/8 sin(3x)*sin(x)
Wäre das dann das Endergebnis… danke für die Hilfe… hab einfach nicht die Lösung in dem Heft nachvollziehen können. ─ akoch 28.12.2021 um 17:26
Wäre das dann das Endergebnis… danke für die Hilfe… hab einfach nicht die Lösung in dem Heft nachvollziehen können. ─ akoch 28.12.2021 um 17:26
Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden.
Cauchy wurde bereits informiert.

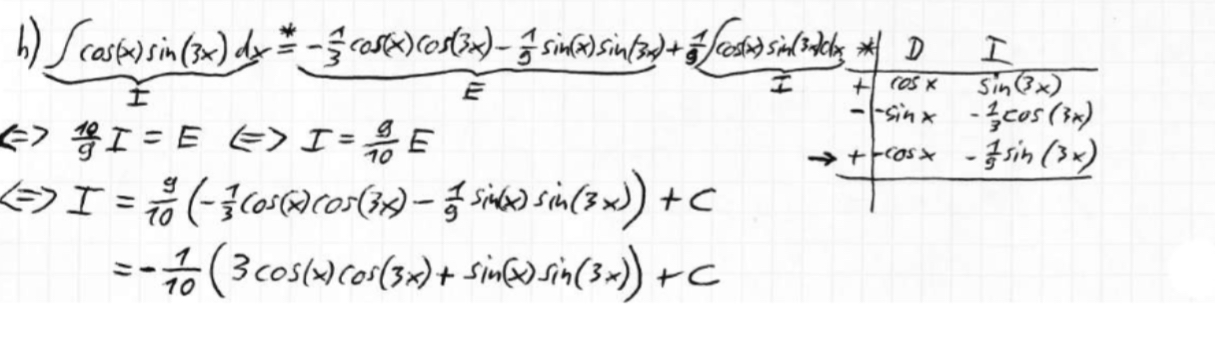 Hier komme ich noch bis zum ersten Schritt aber verstehe nicht wie es zu der 10/9 kommt...
Hier komme ich noch bis zum ersten Schritt aber verstehe nicht wie es zu der 10/9 kommt...