Ist die hier angeführte Menge disjunkt ?

Aufrufe: 405     Aktiv: 30.10.2021 um 21:08
1


-Meiner ersten Überlegung nach ist die Menge disjunkt
-Bei der letzten Restriktion bin ich im Wertebereich von (-Pi/2,Pi/2)
-Wähle dafür x=y
Diese Beschränkung würde dann für x und y gelten
-Finde nun einen Wert größer sin(x) wobei x> y (Mir fällt da keiner ein)


EDIT vom 30.10.2021 um 14:36:

Frage: Enthält die hier aufgeführte Menge nur das leere Element/ Kann für die Menge ein Bereich festgelegt werden für den diese Restriktionen erfüllt werden

EDIT vom 30.10.2021 um 18:32:

Habe meinen Denkfehler bezüglich des negativen Bereichs nun soweit eingesehen - Jedoch ist mir die Begrenzung aufgrund der letzten Restriktion unklar - Ich würde da weiterhin bei PI/2  bleiben 

EDIT vom 30.10.2021 um 18:50:

Wäre das so richtig 

EDIT vom 30.10.2021 um 19:25:

*Wäre es so richtig 

EDIT vom 30.10.2021 um 19:36:

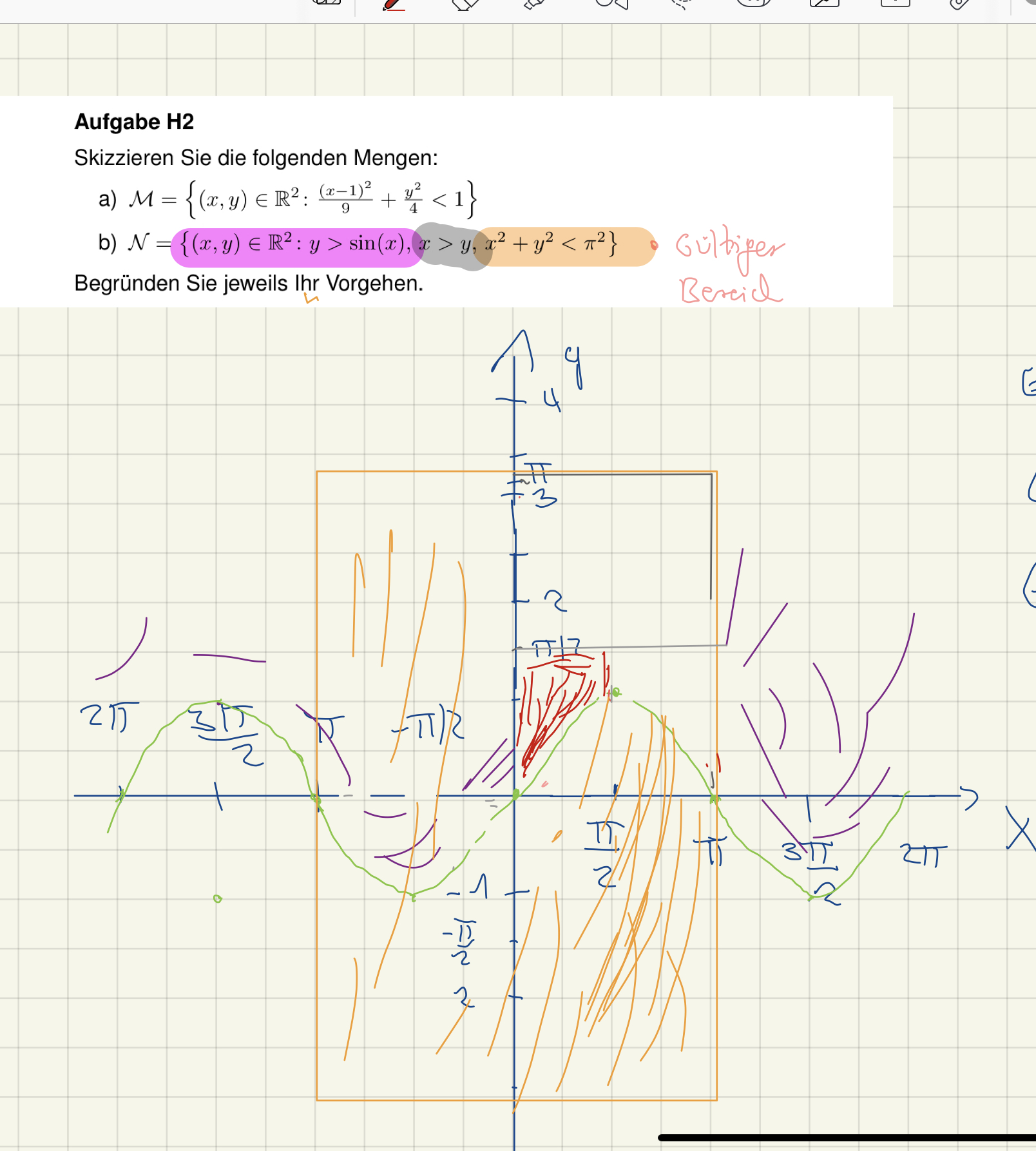
Wäre es so richtig 

EDIT vom 30.10.2021 um 19:43:

Wäre es so richtig 

EDIT vom 30.10.2021 um 20:25:



Wäre es so richtig

EDIT vom 30.10.2021 um 21:05:


Habe nun hoffentlich auch die letzte Restriktion richtig berücksichtigt

EDIT vom 30.10.2021 um 21:08:

*
Diese Frage melden
gefragt
inaktiver Nutzer

 
Kommentar schreiben
1 Antwort
0
Die letzte Bedingung beschreibt eine Kreisscheibe mit dem Radius $\pi$ (ohne Rand). Zeichnen und dann die anderen Bedingungen anschauen.
Diese Antwort melden
geantwortet

Selbstständig, Punkte: 30.55K

 

Leider scheint diese Antwort Unstimmigkeiten zu enthalten und muss korrigiert werden. Cauchy wurde bereits informiert.