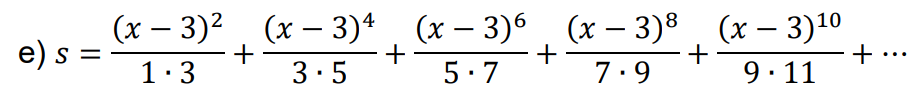Wenn der Konvradius für die Reihe mit $z$ 1 ist (hab ich nicht nachgerechnet) dann bedeutet das: Die Reihe konvergiert für alle $z$ mit $|z|<1$. Dies führt auf $(x-3)^2<1$, was auf $|x-3|<1$ führt, was sich (Zahlengerade!, Betrag ist Abstand auf der Zahlengeraden) problemlos zu $2<x<4$ umstellen lässt.
Lehrer/Professor, Punkte: 38.86K