1
Ah, du willst eine explizite Darstellung haben. An welchen Stellen stehen die 1sen? So solltest du leicht auf eine kompakte Form kommen.
─
orbit
18.11.2021 um 17:37
Danke für die Antwort, die Einsen sethen ja in dem Beispiel an jeder zweierpotenz, allerdings bekomme ich leider keine Kompakte Form hin :(
─ usere8cf9f 18.11.2021 um 20:18
─ usere8cf9f 18.11.2021 um 20:18
Ja aber genau das ist es doch. $a_n=\begin{cases}1 & n=2^{k}, k\in \mathbb{N}\\0 & \text{sonst}\end{cases}$.
─
orbit
18.11.2021 um 20:44
Oh, Danke war mir nicht sicher wie man das Aufschreiben soll, du hast mir sehr geholfen
─ usere8cf9f 18.11.2021 um 20:50
─ usere8cf9f 18.11.2021 um 20:50

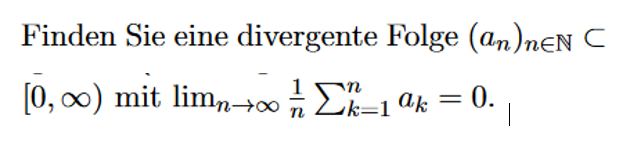
─ usere8cf9f 18.11.2021 um 17:11