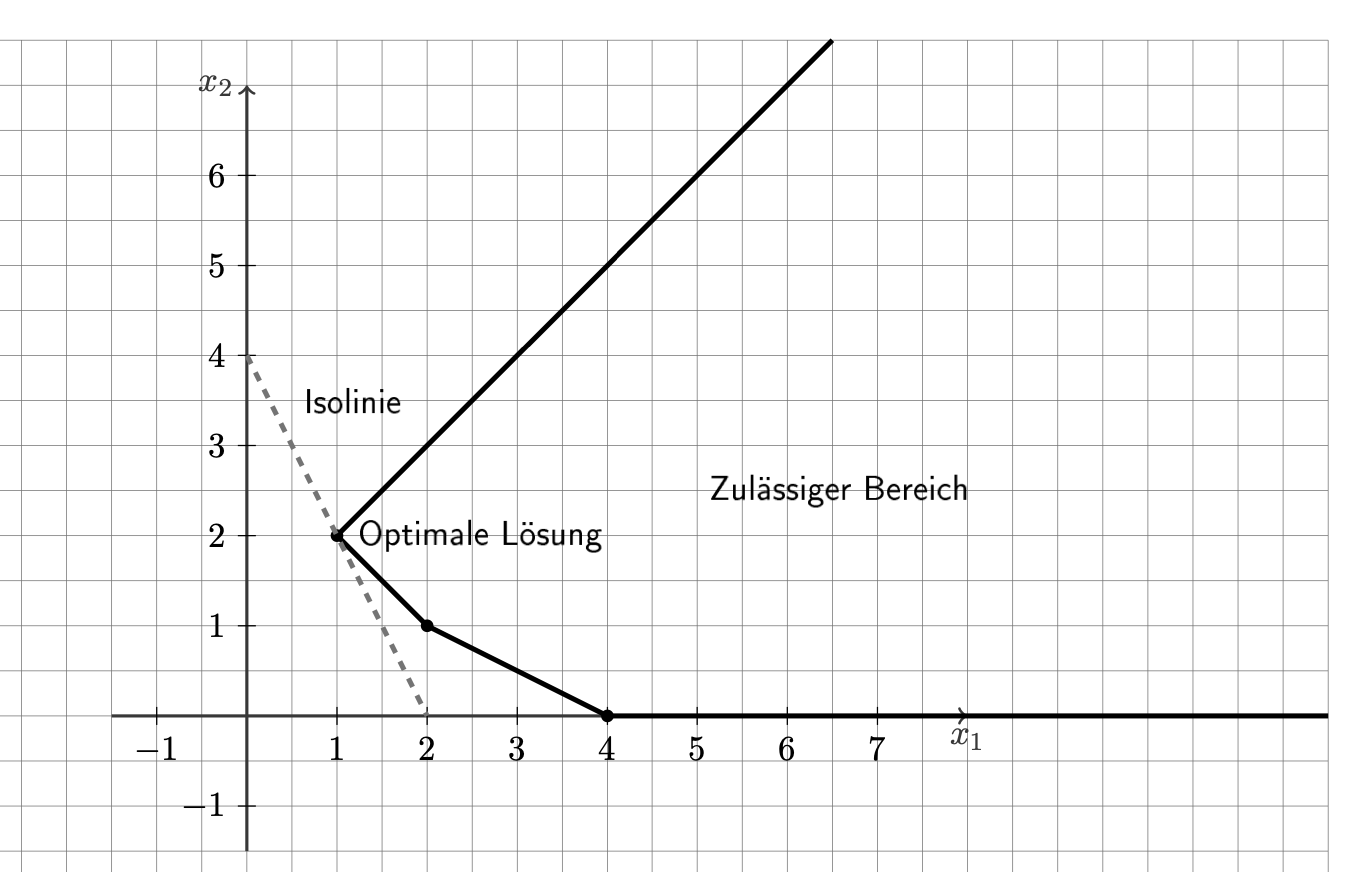
Um ein lineares Optimierungsproblem graphisch zu lösen, kannst du eine Gerade nehmen, die senkrecht auf der Zielfunktion, interpretiert als Vektor, steht, und diese solange verschieben, bis der zulässige Bereich gerade noch draufliegt. In diesem Fall haben wir die Geraden $2x_1+x_2=k$. Alle Punkte, die auf einer solchen Geraden liegen, haben den gleichen Wert $k$ der Zielfunktion, also brauchen wir die Gerade mit dem kleinsten $k$, die nichtleeren Schnitt mit dem zulässigen Bereich hat. Dazu verschieben wir die Gerade solange nach links, dass sie gerade noch den Rand berührt. Das ist dann die eingezeichnete Isolinie, die den zulässigen Bereich in der optimalen Lösung schneidet.