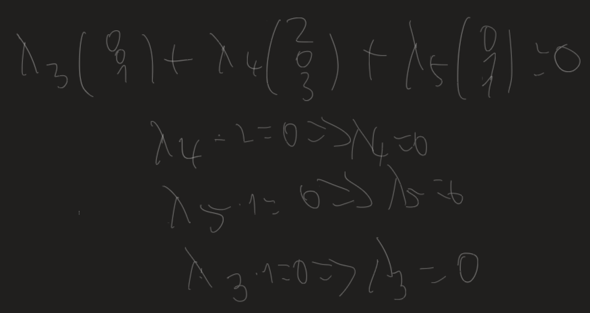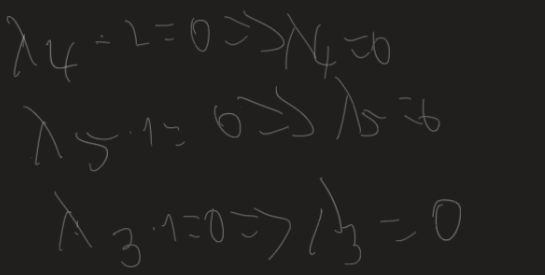Für linear unabhängige Vektoren gilt, dass die Linearkombination nur dann den Nullvektor ergibt, wenn alle Koeffizienten der Linearkombination auf 0 gesetzt werden.

$\lambda_4\cdot2=0$ lässt sich umformen zu $\lambda_4=0$. Die anderen Gleichungen durch Einsetzen und Umformen lösen. $\lambda_5=0$ ist etwas schlampig geschrieben. Sieht aus wie $6$.

Die Indizes an den Lambdas kennst du bereits von der Nullstellenbestimmung. Da hast du ja auch $x_1$, $x_2$, ... für deine Nullstellen. Man muss die Koeffizienten ja unterscheiden.

Grundsätzlich zeigst du die lineare Unabhängigkeit von Vektoren, indem du die Linearkombination aufstellst und diese gleich dem Nullvektor setzt. Dann Zeilenweise die Gleichungen mit den Koeffizienten als Variablen schreiben und lösen. Ist die einzige Lösung $\lambda_3=\lambda_4=\lambda_5=0$, sind die Vektoren linear unabhängig. Gibt es eine/mehrere andere Lösung(en), sind sie linear abhängig.